Representing Uncertainty
Data Visualization and Exploration
Measuring the real world
Measuring is a noisy process.
Probability theory and statistics give us the tools to deal with the noise.
Basic probability theory
Events and probability
Sample space: the set of outcomes of some experiment (denoted with \(\Omega\)).
Event: a subset of the sample space ( \(A \subseteq \Omega\) ).
Probability: a probability function \(P\) on a finite sample space assigns to each event \(A \subseteq \Omega\) a number \(P(A)\) in \([0,1]\) such that
- \(P(\Omega) = 1\),
- \(P(A \cup B) = P(A) + P(B)\) if \(A\) and \(B\) are disjoint.
Example: coin tosses \(\Omega = \{H, T\}\)
Example: dice roll \(\Omega = \{1,2,3,4,5,6\}\)
Example: 2 coin tosses \(\Omega = \{(H, H), (H, T), (T, H), (T, T)\}\)
Discrete random variables
Let \(\Omega\) be a sample space. A discrete random variable is a function
\[\begin{equation} X : \Omega \to \mathbb{R} \end{equation}\]that takes on a (possibly infinite) discrete set of values \(a_1, a_2, \dots\)
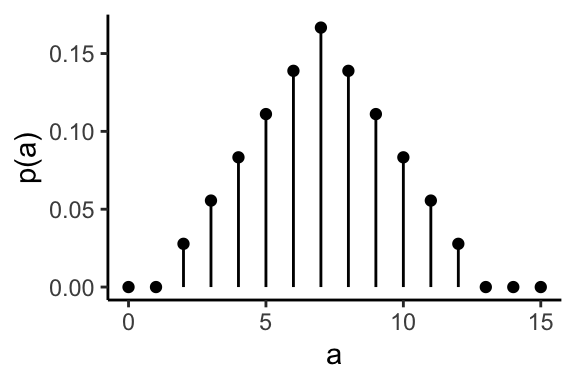
Example: throwing two dices and add them.
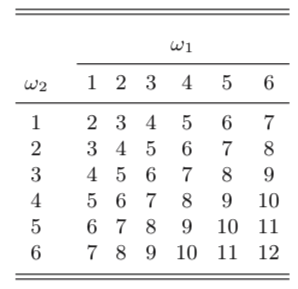
Probability mass function
The probability mass function \(p\) of a discrete random variable \(X\) is the function
\[\begin{equation} p(a) = P(X = a) \quad \text{for} -\infty < a < \infty \end{equation}\]The probability mass of the sum of two dice.
Discrete random variables
Discrete random variables make it easier to reason about complex events by mapping them to numbers on the real line, to which we then assign probabilities.
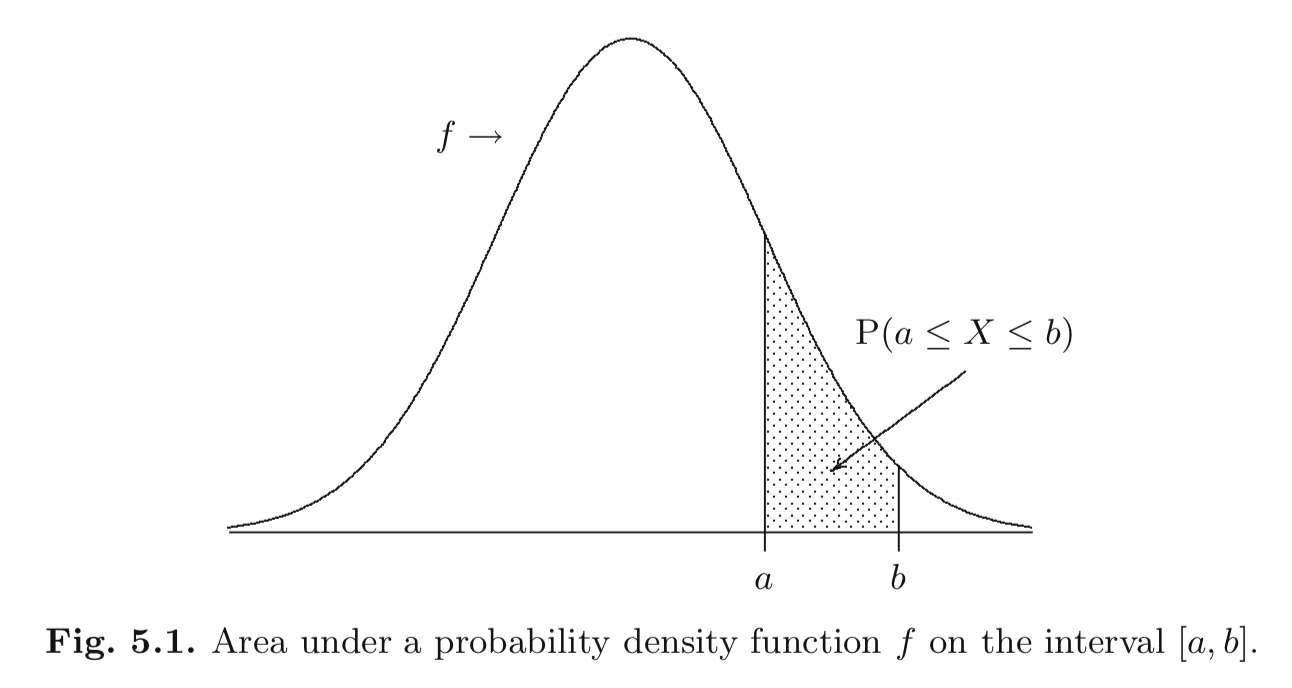
Continuous random variables
A random variable \(X\) is continuous if
for some function \(f : \mathbb{R} \to \mathbb{R}\) and for any numbers \(a\) and \(b\) with \(a < b\),
\[\begin{equation} P(a \le X \le b) = \int_a^b f(x) d x \end{equation}\]and \(f(x) \ge 0~\forall x\in \mathbb{R}\) and \(\int_{-\infty}^{\infty} f(x) d x = 1\).
The function \(f\) is the probability density function.
Continuous random variables
Expectation (aka Mean)
Intuitively, it is the average of a large number of independent realizations of the random variable.
More formally, it’s the weighted average of all the values taken by the random variable.
Discrete RV
Continuous RV
\[\begin{equation} E[X] = \int_{-\infty}^{\infty} x f(x)~dx \end{equation}\]Variance and standard deviation
The variance represents the spread of a random variable around its mean.
\[\begin{equation} Var(X) = E[(X - E[X])^2] \end{equation}\]“Expected squared deviation from the mean.”
It is always positive.
The standard deviation is the square root of the variance: \(\sqrt{Var(X)}\).
It is always positive.
Quantiles
Let \(X\) be a continuous random variable and let \(p \in [0,1]\).
The \(p\)-th quantile is the smallest \(q\) such that:
\[\begin{equation} P[X \le q] = p \end{equation}\]The \(0.5\)-quantile is called the median.
What is the \(1.0\)-quantile?
Percentiles
In many contexts we will use the term percentile instead of quantile. Just multiply \(p\) by 100.
- \(0.3\)-quantile \(\rightarrow\) 30th percentile
- \(0.75\)-quantile \(\rightarrow\) 75th percentile
- median \(\rightarrow\) 50th percentile
Can you rephrase the concept of quantile/percentile?
Definition: The \(p\)-th quantile is the smallest \(q\) such that \(P[X \le q] = p\).
Rephrasing: The \(p\)-th quantile is the smallest \(q\) such that \(100p\%\) of the distribution is below \(q\).
Order statistics
Consider a dataset \(x_1, x_2, \dots, x_n\).
The \(k\)-th order statistic is the \(k\)-th smallest element, which is denoted with \(x_{(k)}\).
How can you compute it?
Order statistics and empirical quantiles
We assume that the \(i\)th order statistic is the \(i/(n+1)\) quantile (ordered).
To compute empirical quantiles you linearly interpolate between order statistics.
Let \(0 < p < 1\).
We want to compute the \(p\)th empirical quantile, \(q(p)\), for a dataset \(x_1,x_2,\ldots,x_n\).
We denote the integer part of \(a\) by \(\lfloor a \rfloor\).
Let \(k = \lfloor p . (n+1) \rfloor\) and \(\alpha = p . (n+1) - k\)
\[\begin{equation} q(p) = x_{(k)} + \alpha . (x_{(k+1)} - x_{(k)}) \end{equation}\]Exercise: 41 41 41 41 41 42 43 43 43 58 58
Compute the 55-empirical percentile.
Order statistics and quantiles example
Order statistics and quantiles example
Order statistics and quantiles example
Order statistics and quantiles example
Random sample
A random sample is a collection of \(n\) random variables
\[\begin{equation} X_1, X_2, \dots, X_n \end{equation}\]that have the same distribution and are mutually independent.
We can use random sampling to model a repeated measurement of some unknown quantity.
The actual instantiation of a random sample is called a realization.
Dealing with random samples
- When you measure something, you usually don’t know the underlying distribution.
Your random sample is a realization of this unknown distribution.
You want to derive conclusions about the true distribution.
However, you can perform computations only on values in your data.
It’s like trying to assess some facts about the world looking at an imperfect mirror.
Many datasets can be modeled as realizations of random samples.
Estimators
An estimate is a value that only depends on the dataset \(x_1, \dots, x_n\), i.e., it is some function of the dataset only.
The mean is:
\[\begin{equation} \bar{x} = \frac{\sum_i x_i}{n} \end{equation}\]In R: mean
The variance is:
\[\begin{equation} \bar{s} = \frac{\sum_i (x_i - \bar{x})^2}{n-1} \end{equation}\]In R: var.
The standard deviation in R is sd.
Confidence intervals
We know that the sample mean is an estimator to the true mean \(\mu\).
How good is this estimator? How does quality relate to the number of samples?
The law of large numbers
If \(\bar{X}\) is the average of \(n\) independent random variables with expectation \(\mu\), then for any \(\varepsilon > 0\): \[\begin{equation} \lim_{n \to \infty} P(|\bar{X} - \mu| > \varepsilon) = 0 \end{equation}\]
This means that when we take a very large random sample, the arithmetic average is a good estimator of the value of the mean \(\mu\).
Repeated experiments
We are going to make statements about taking a random sample of size \(n\) repeatedly.
This is equivalent to running an experiment, defined as a batch of measurements, several times, getting every time different outcomes.
Repeated experiments
Example: consider 6 datasets of size \(n=4\), taken as realizations of the same random sample.
| dataset |
|---|
| 0.393, 0.581, -1.231, 0.661 |
| 0.773, -1.422, -0.673, -0.070 |
| 0.758, 1.041, 0.200, -1.208 |
| 0.849, 0.878, -1.260, -0.114 |
| -0.740, 1.037, 2.064, 0.697 |
| -3.326, 0.499, -1.006, -0.534 |
Estimating the mean
The sample mean of each dataset is an estimate of the true mean \(\mu\) of the random sample.
| dataset | estimate |
|---|---|
| 0.393, 0.581, -1.231, 0.661 | 0.10100 |
| 0.773, -1.422, -0.673, -0.070 | -0.34800 |
| 0.758, 1.041, 0.200, -1.208 | 0.19775 |
| 0.849, 0.878, -1.260, -0.114 | 0.08825 |
| -0.740, 1.037, 2.064, 0.697 | 0.76450 |
| -3.326, 0.499, -1.006, -0.534 | -1.09175 |
Estimating the mean
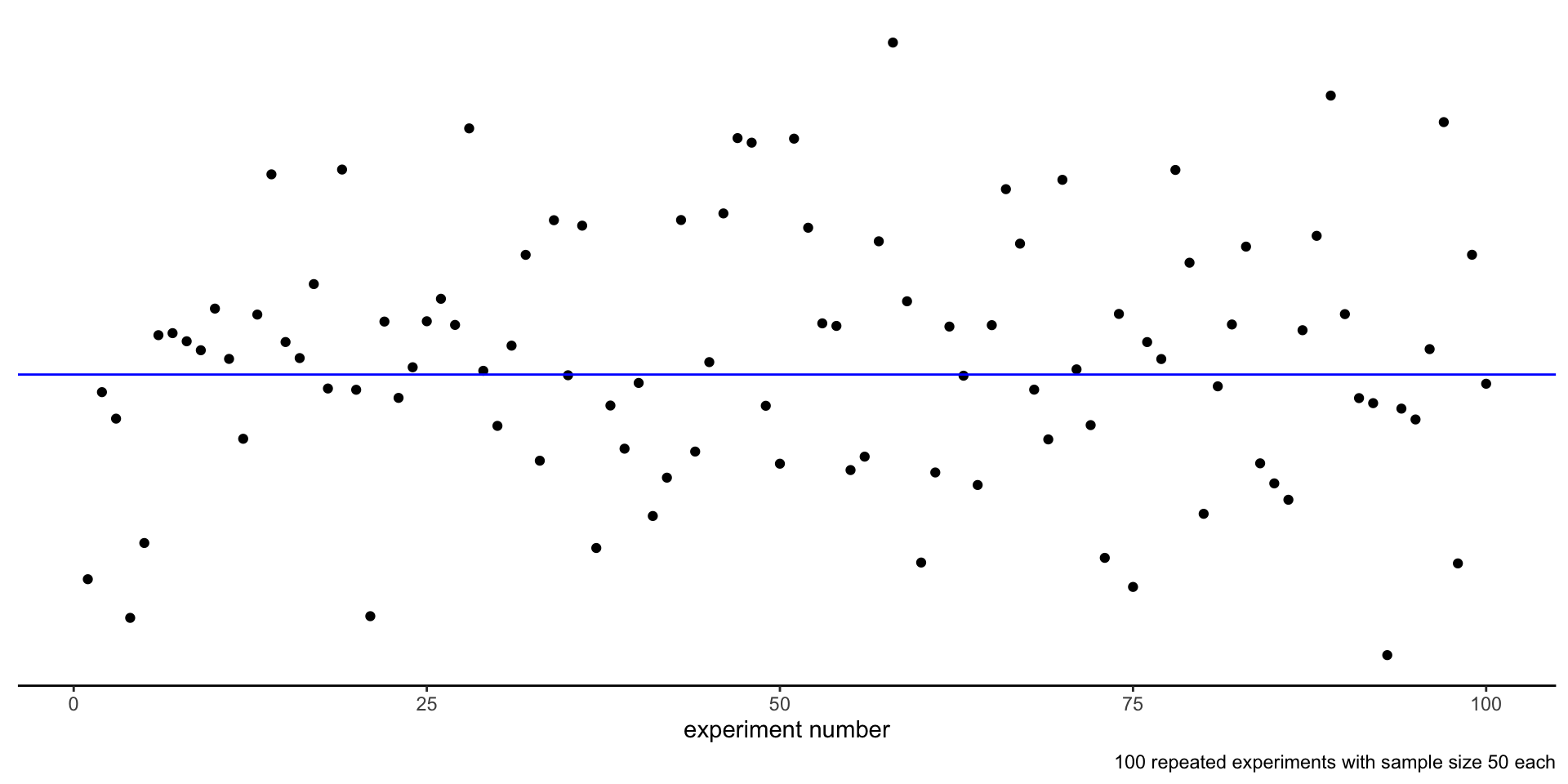
How confident are we in our estimates?
Instead of just relying on a single number (the sample mean) we might want to derive an interval.
Consider a dataset \(x_1, \dots, x_n\), modeled as realization of random variables \(X_1, \dots, X_n\) with mean \(\mu\).
Let \(\gamma \in [0,1]\).
If there exists \(L_n = g(X_1, \dots, X_n)\) and \(U_n = h(X_1, \dots, X_n)\) such that:
\[\begin{equation} P( L_n \le \mu \le U_n ) \ge \gamma \end{equation}\]then the interval \((l_n, u_n)\)
with \(l_n = g(x_1, \dots, x_n)\) and \(u_n=h(x_1, \dots, x_n)\) is a
\(100\gamma\)% confidence interval for \(\mu\).
\(\gamma\) is called the confidence level.
An example
Observation: each time we run the experiment, we derive a different confidence interval.
| dataset | lower | upper |
|---|---|---|
| 0.393, 0.581, -1.231, 0.661 | -0.75800 | 0.64100 |
| 0.773, -1.422, -0.673, -0.070 | -1.08400 | 0.41150 |
| 0.758, 1.041, 0.200, -1.208 | -0.71650 | 0.89950 |
| 0.849, 0.878, -1.260, -0.114 | -0.73275 | 0.86350 |
| -0.740, 1.037, 2.064, 0.697 | -0.29575 | 1.72225 |
| -3.326, 0.499, -1.006, -0.534 | -2.62800 | 0.12275 |
An example
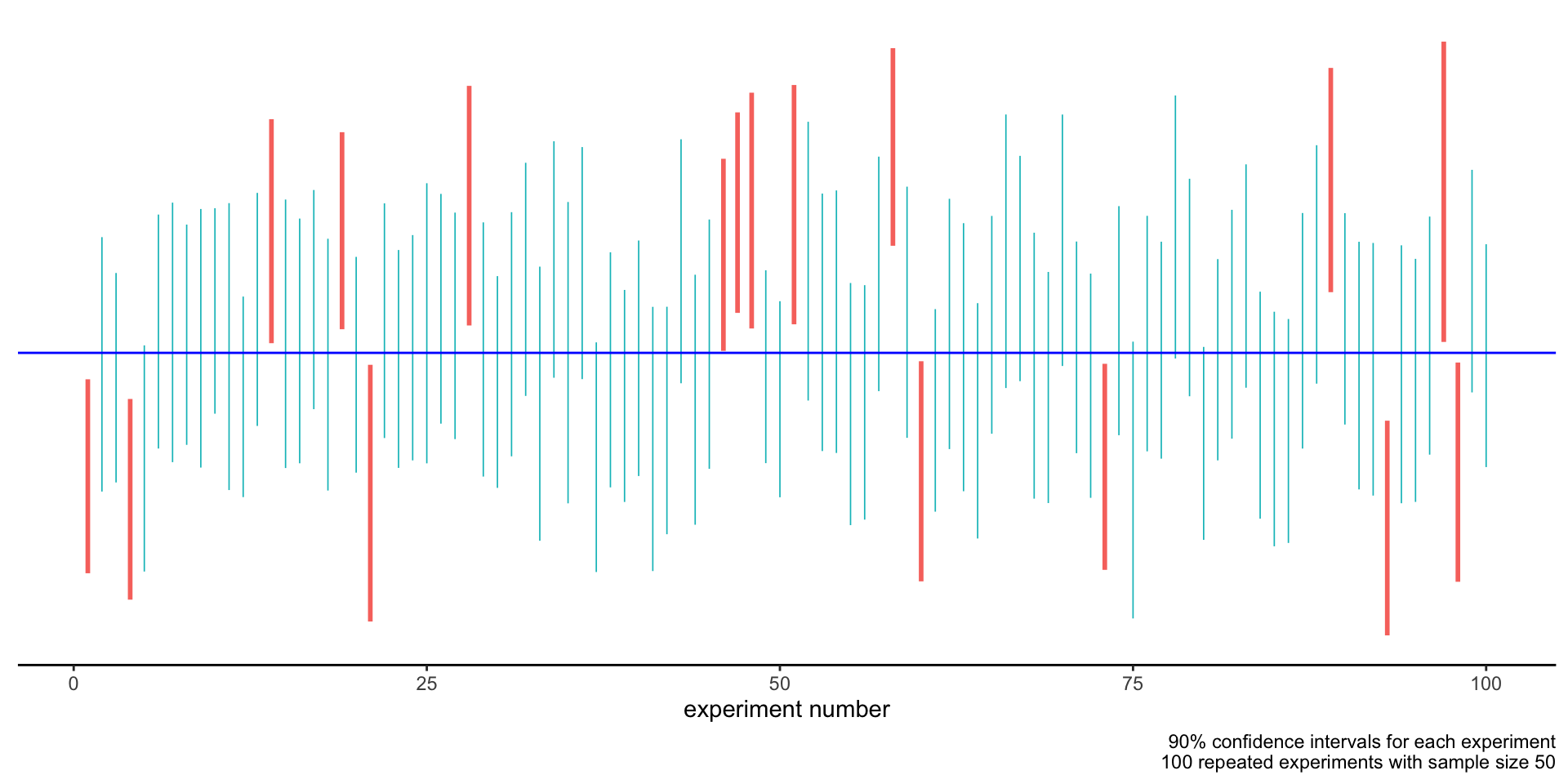
Building confidence intervals
In the general case confidence intervals are built using a technique called bootstrapping.
\(c^*_u\) and \(c^*_l\) are related to the confidence level \(\gamma\).
\(\bar{x}\) is the sample mean.
\(s_n\) is the sample standard deviation.
\(n\) is the number of samples.
How does changing the size \(n\) of the sample change the confidence interval, for fixed \(\gamma\)?
How does changing the confidence level \(\gamma\) change the confidence interval, for fixed \(n\)?
For fixed \(\gamma\), increasing \(n\) narrows the intervals.
For fixed \(n\), increasing \(\gamma\) widens the intervals.
What does this all mean?
- The confidence interval we derive from a dataset is itself the realization of a random variable.
Such a random interval has a probability \(\gamma\) of containing the population mean \(\mu\).
The probability statement is on the random variable defining the interval, not on its realization!
What does this all mean?
For a fixed dataset we can build a confidence interval. Both are realizations of random variables.
We can say:
We are 90% confident that the interval contains \(\mu\).
The confidence interval is generated by a random variable that 90% of the time gives an interval containing \(\mu\).
We cannot say:
The interval contains \(\mu\) with probability 90%.
The interval either contains \(\mu\) or not: that’s a deterministic fact we cannot know.
How to build confidence intervals with R
Use the function mean_cl_boot(data, conf.int=..confidence level..)
In data pipelines
the result will contain three new columns:
y(average),ymin(lower bound of confidence interval),ymax(upper bound of confidence interval).
Example: measuring the speed of light
| Expt | Run | Speed |
|---|---|---|
| 1 | 1 | 299850 |
| 1 | 2 | 299740 |
| 1 | 3 | 299900 |
| 1 | 4 | 300070 |
| 1 | 5 | 299930 |
| 1 | 6 | 299850 |
| 1 | 7 | 299950 |
| 1 | 8 | 299980 |
| 1 | 9 | 299980 |
| 1 | 10 | 299880 |
| 1 | 11 | 300000 |
| 1 | 12 | 299980 |
| 1 | 13 | 299930 |
| 1 | 14 | 299650 |
| 1 | 15 | 299760 |
| 1 | 16 | 299810 |
| 1 | 17 | 300000 |
| 1 | 18 | 300000 |
| 1 | 19 | 299960 |
| 1 | 20 | 299960 |
| 2 | 1 | 299960 |
| 2 | 2 | 299940 |
| 2 | 3 | 299960 |
| 2 | 4 | 299940 |
| 2 | 5 | 299880 |
| 2 | 6 | 299800 |
| 2 | 7 | 299850 |
| 2 | 8 | 299880 |
| 2 | 9 | 299900 |
| 2 | 10 | 299840 |
| 2 | 11 | 299830 |
| 2 | 12 | 299790 |
| 2 | 13 | 299810 |
| 2 | 14 | 299880 |
| 2 | 15 | 299880 |
| 2 | 16 | 299830 |
| 2 | 17 | 299800 |
| 2 | 18 | 299790 |
| 2 | 19 | 299760 |
| 2 | 20 | 299800 |
| 3 | 1 | 299880 |
| 3 | 2 | 299880 |
| 3 | 3 | 299880 |
| 3 | 4 | 299860 |
| 3 | 5 | 299720 |
| 3 | 6 | 299720 |
| 3 | 7 | 299620 |
| 3 | 8 | 299860 |
| 3 | 9 | 299970 |
| 3 | 10 | 299950 |
| 3 | 11 | 299880 |
| 3 | 12 | 299910 |
| 3 | 13 | 299850 |
| 3 | 14 | 299870 |
| 3 | 15 | 299840 |
| 3 | 16 | 299840 |
| 3 | 17 | 299850 |
| 3 | 18 | 299840 |
| 3 | 19 | 299840 |
| 3 | 20 | 299840 |
| 4 | 1 | 299890 |
| 4 | 2 | 299810 |
| 4 | 3 | 299810 |
| 4 | 4 | 299820 |
| 4 | 5 | 299800 |
| 4 | 6 | 299770 |
| 4 | 7 | 299760 |
| 4 | 8 | 299740 |
| 4 | 9 | 299750 |
| 4 | 10 | 299760 |
| 4 | 11 | 299910 |
| 4 | 12 | 299920 |
| 4 | 13 | 299890 |
| 4 | 14 | 299860 |
| 4 | 15 | 299880 |
| 4 | 16 | 299720 |
| 4 | 17 | 299840 |
| 4 | 18 | 299850 |
| 4 | 19 | 299850 |
| 4 | 20 | 299780 |
| 5 | 1 | 299890 |
| 5 | 2 | 299840 |
| 5 | 3 | 299780 |
| 5 | 4 | 299810 |
| 5 | 5 | 299760 |
| 5 | 6 | 299810 |
| 5 | 7 | 299790 |
| 5 | 8 | 299810 |
| 5 | 9 | 299820 |
| 5 | 10 | 299850 |
| 5 | 11 | 299870 |
| 5 | 12 | 299870 |
| 5 | 13 | 299810 |
| 5 | 14 | 299740 |
| 5 | 15 | 299810 |
| 5 | 16 | 299940 |
| 5 | 17 | 299950 |
| 5 | 18 | 299800 |
| 5 | 19 | 299810 |
| 5 | 20 | 299870 |
Let’s replicate the experiment of Michelson and Morley (1887).
Assumption: the measurements are a realization of a random sample.
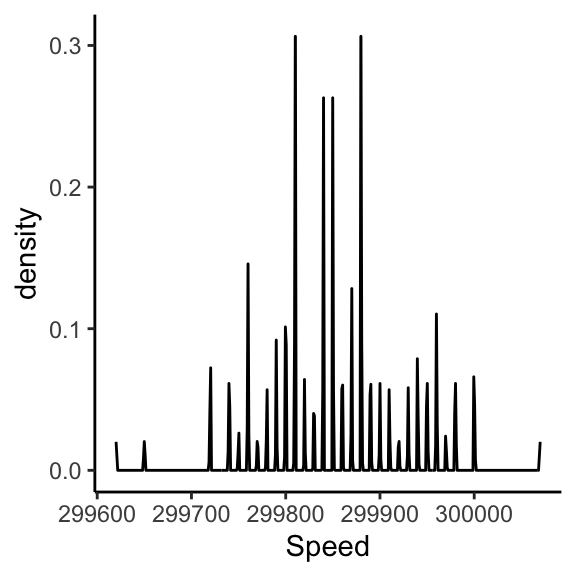
Visualizing the measurements: rug
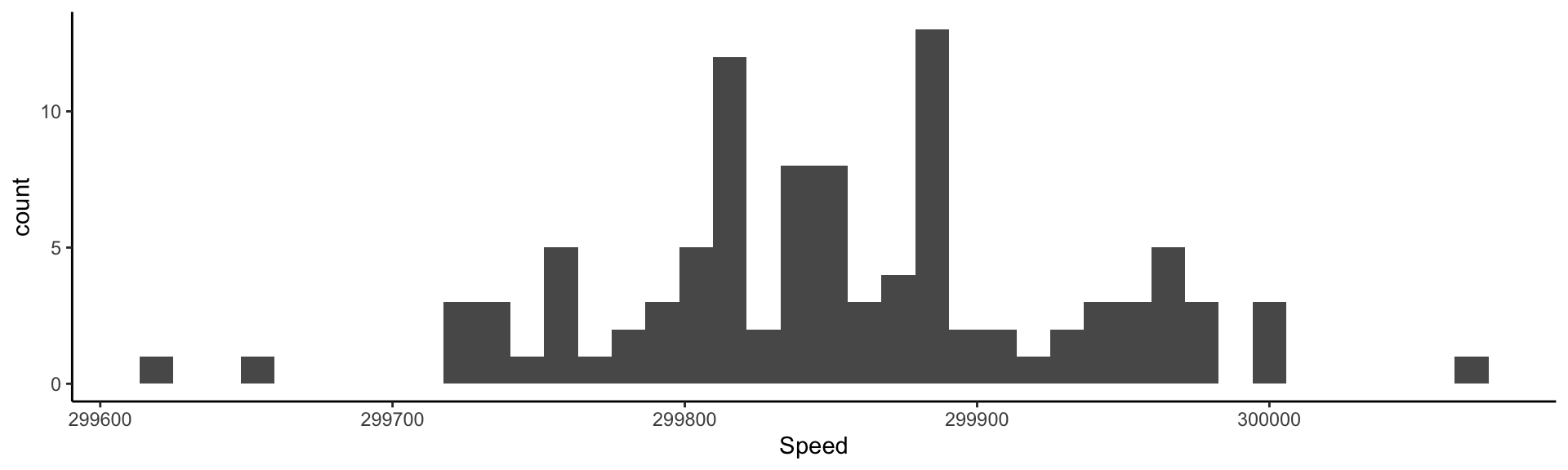
Visualizing the measurements: histogram
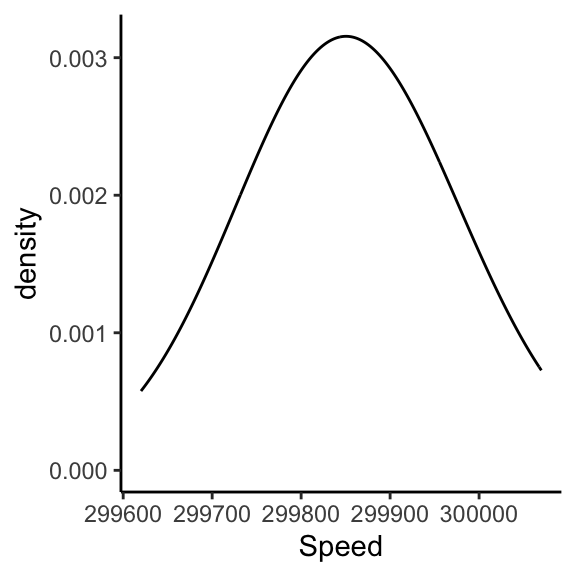
Visualizing the measurements: Kernel Density Estimate
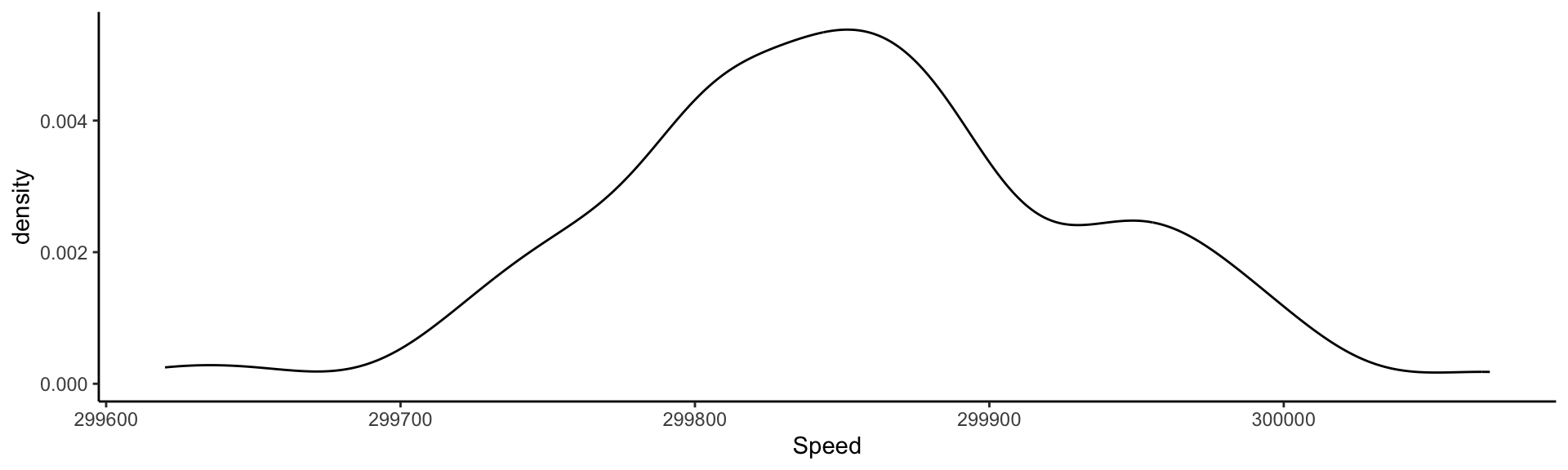
This is an estimate of the Probability Density Function derived from data.
Visualizing the measurements: Kernel Density Estimate
Visualizing the measurements: adding information
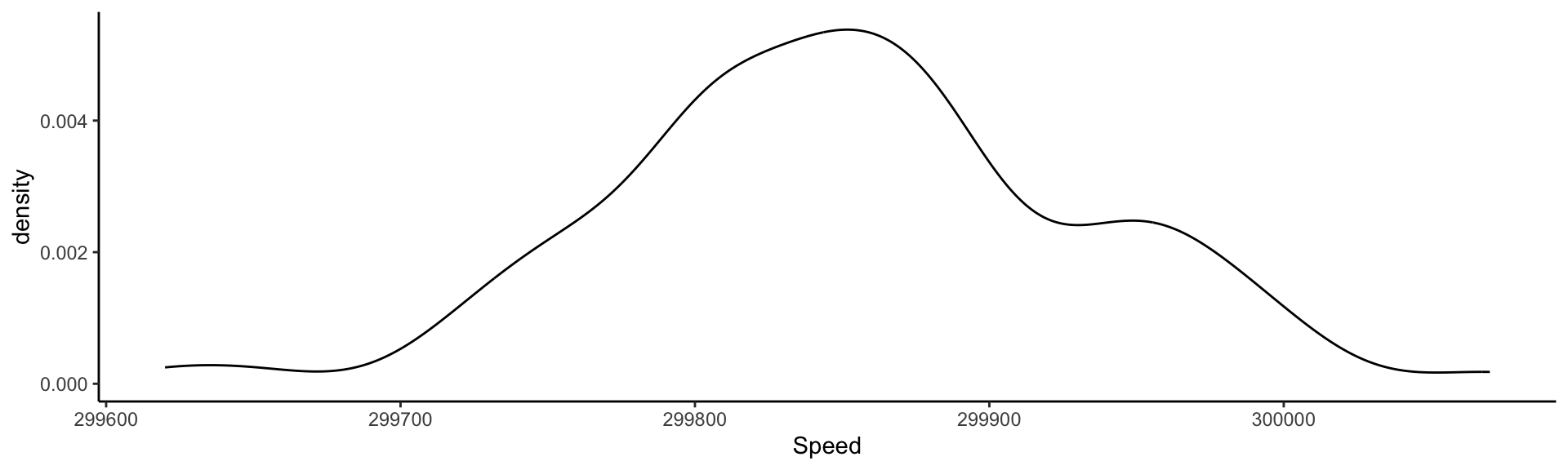
Visualizing the measurements: adding information
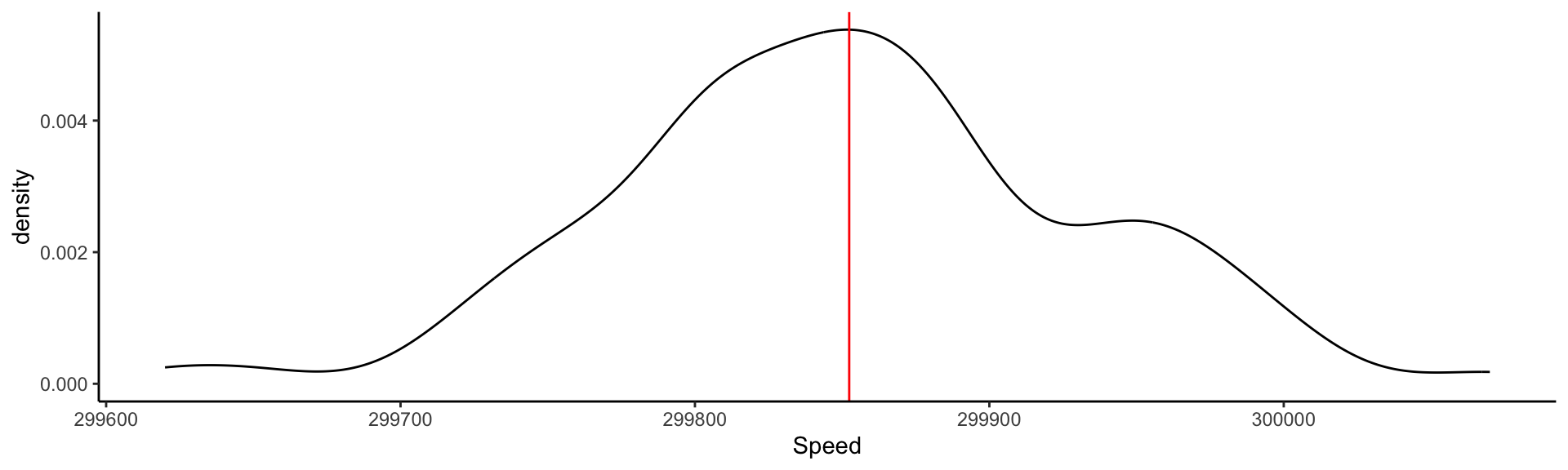
Visualizing the measurements: adding information
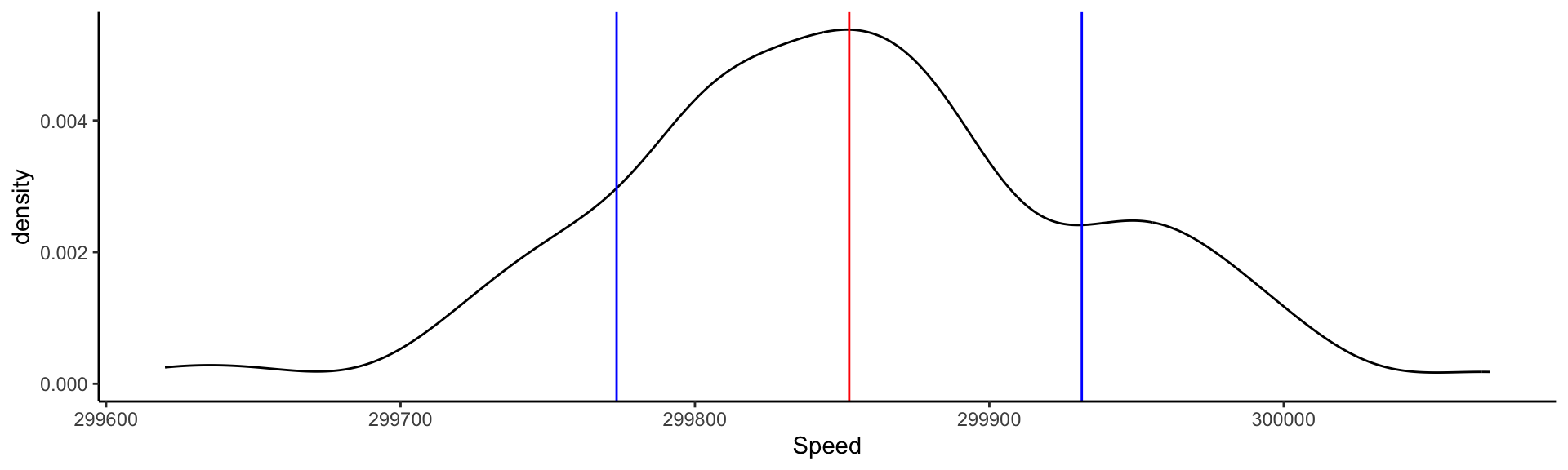
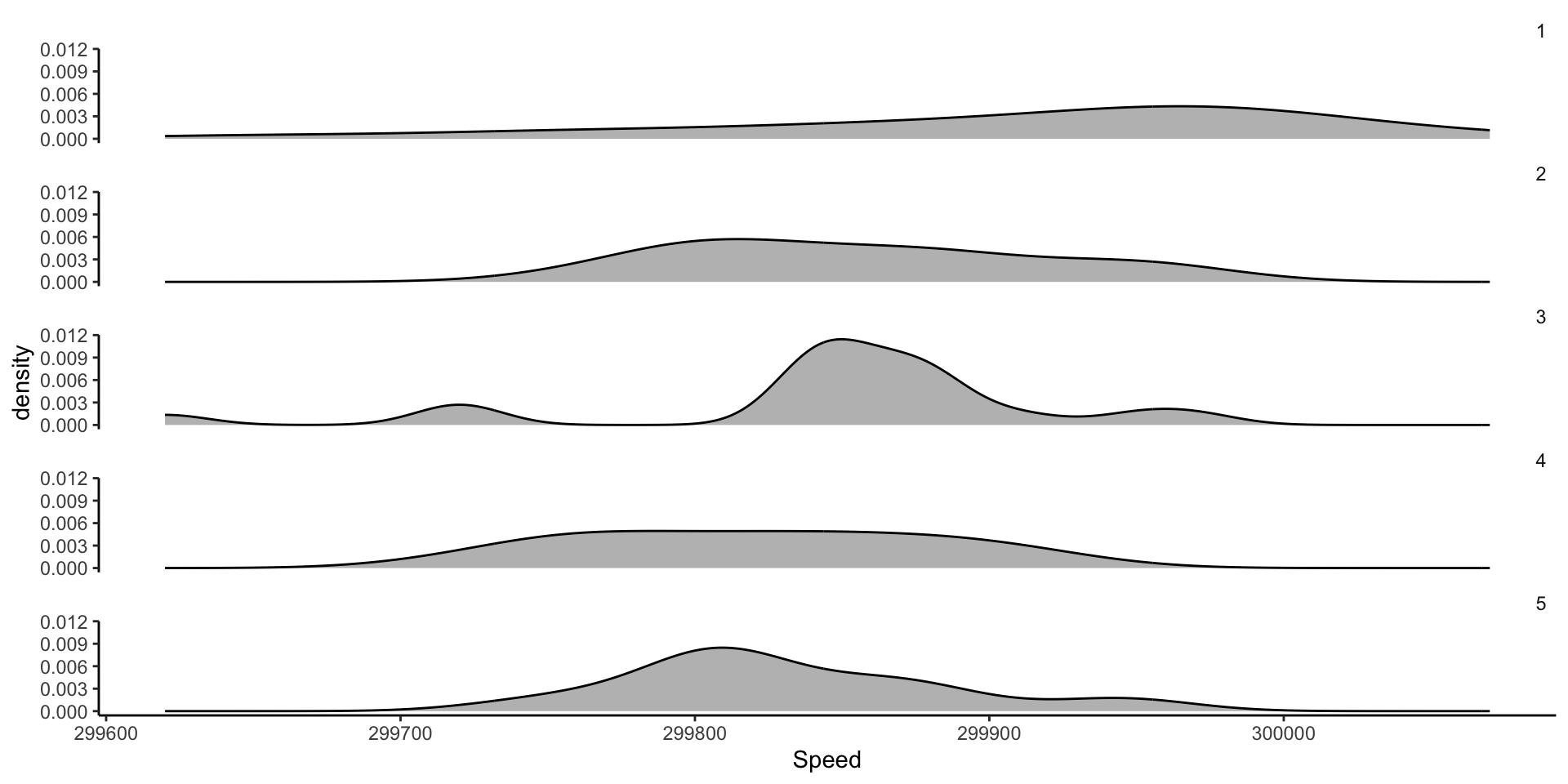
Comparing different experiments: faceting KDEs
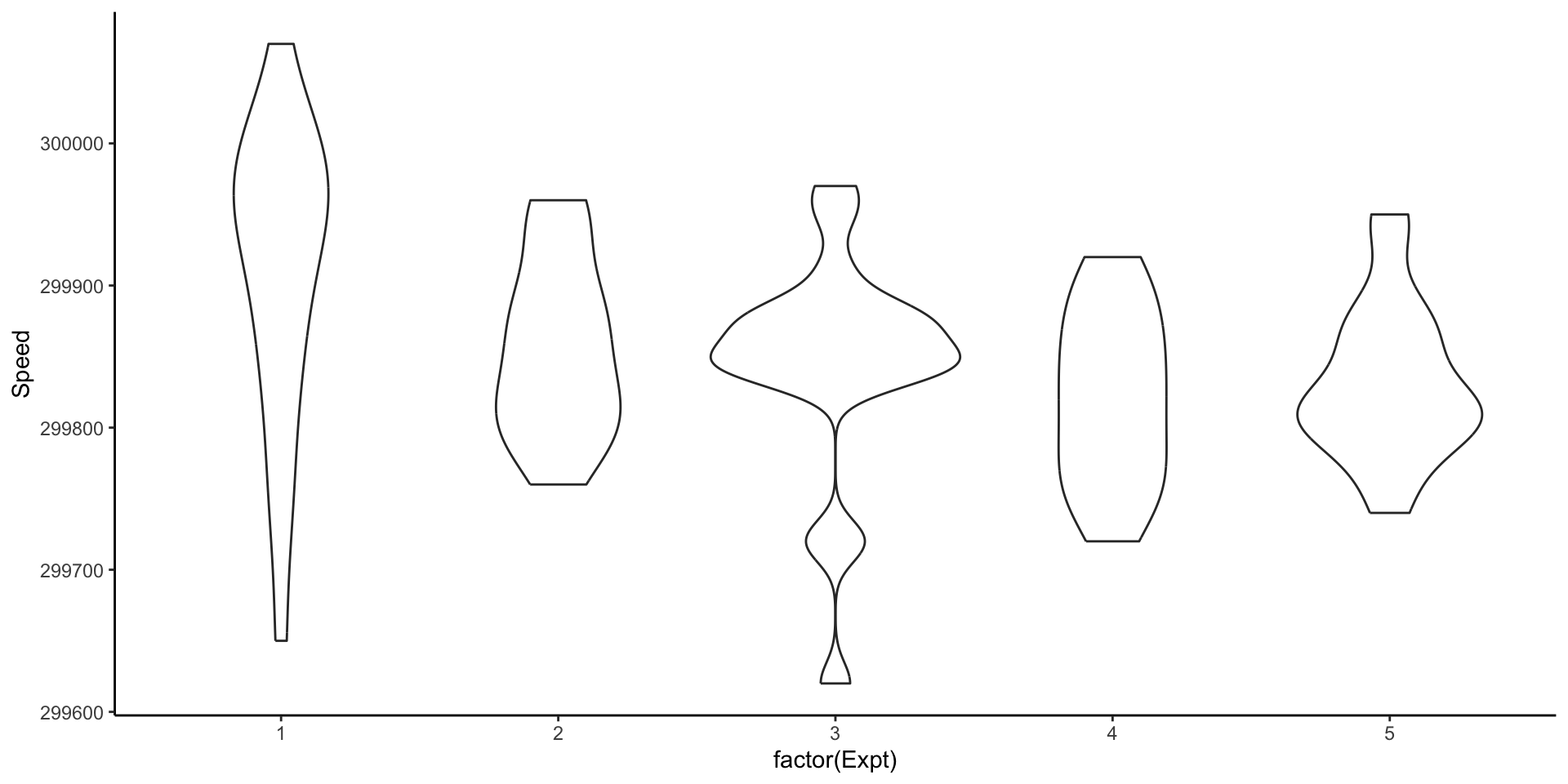
Comparing different experiments: violin plots
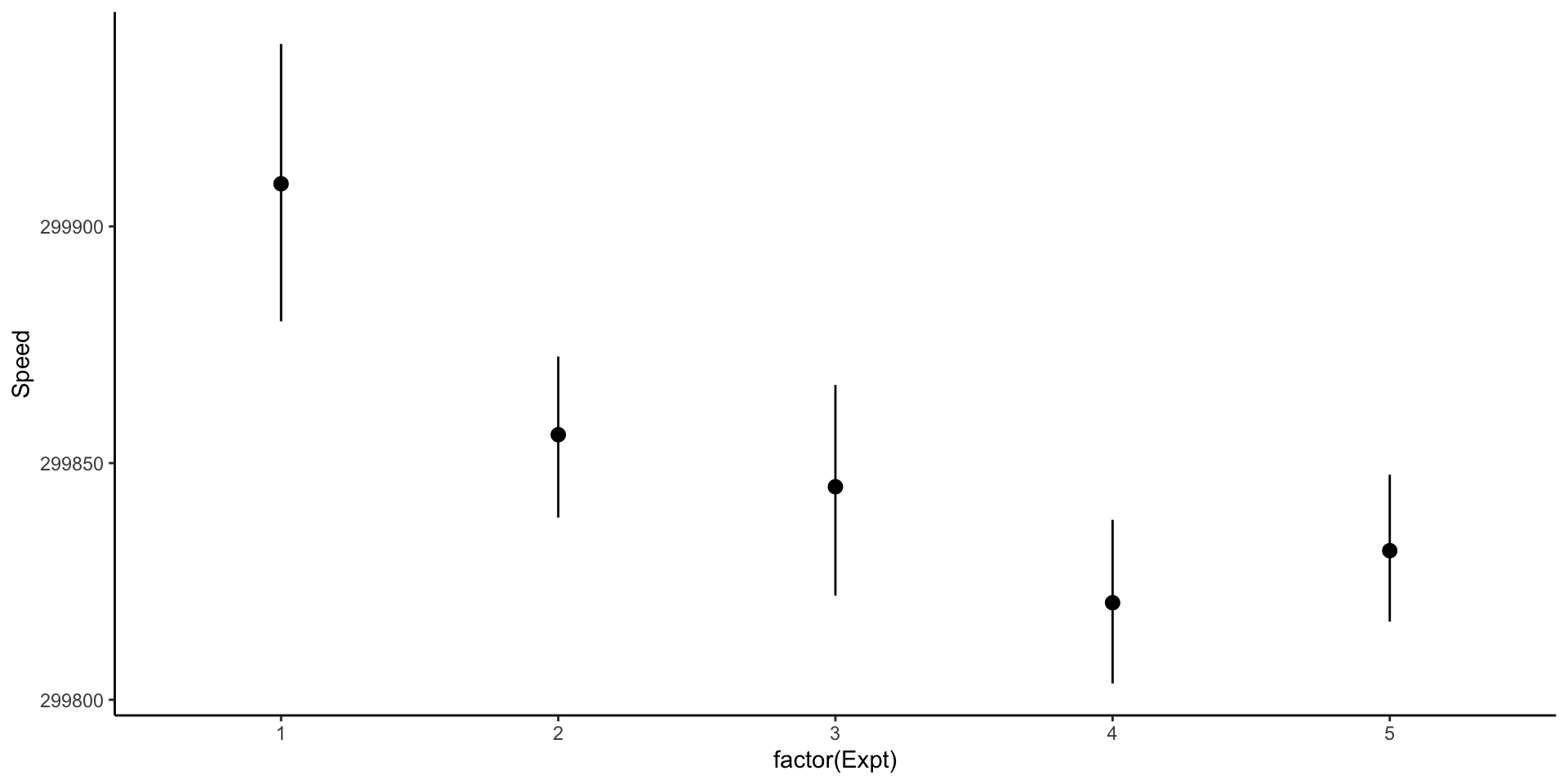
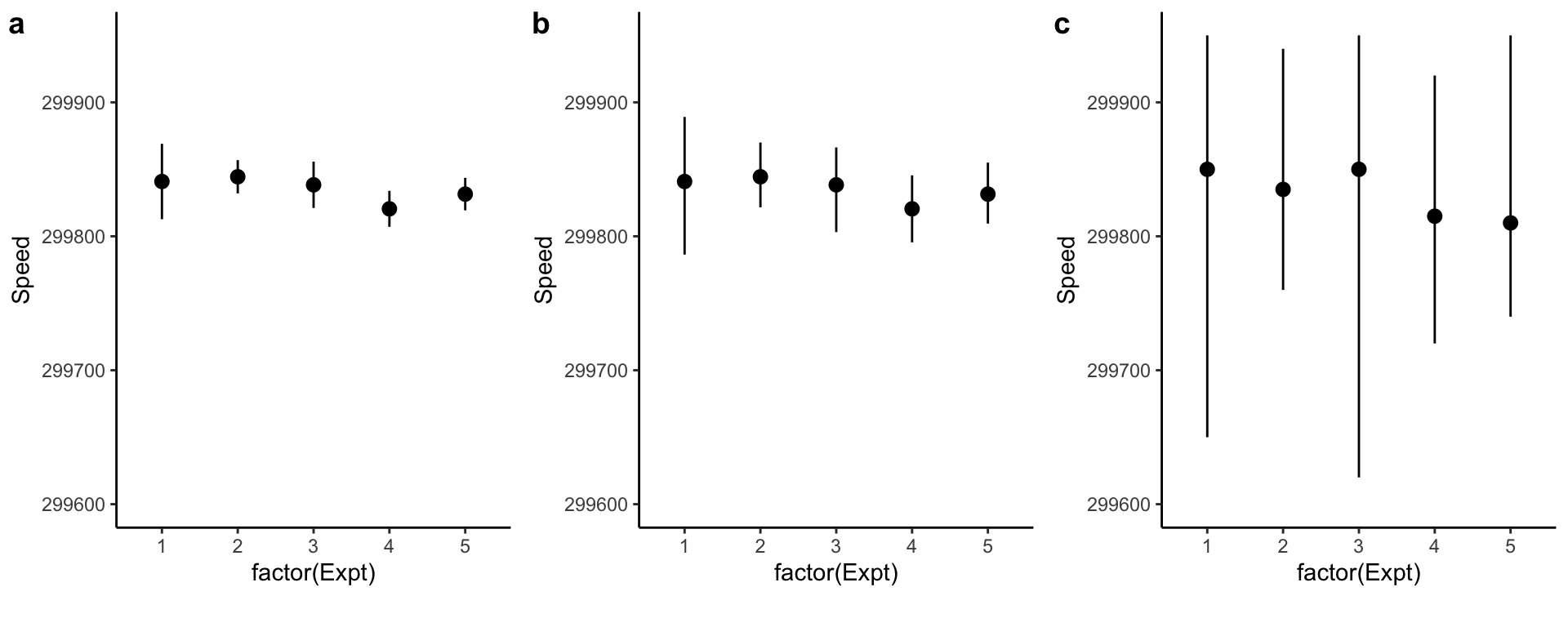
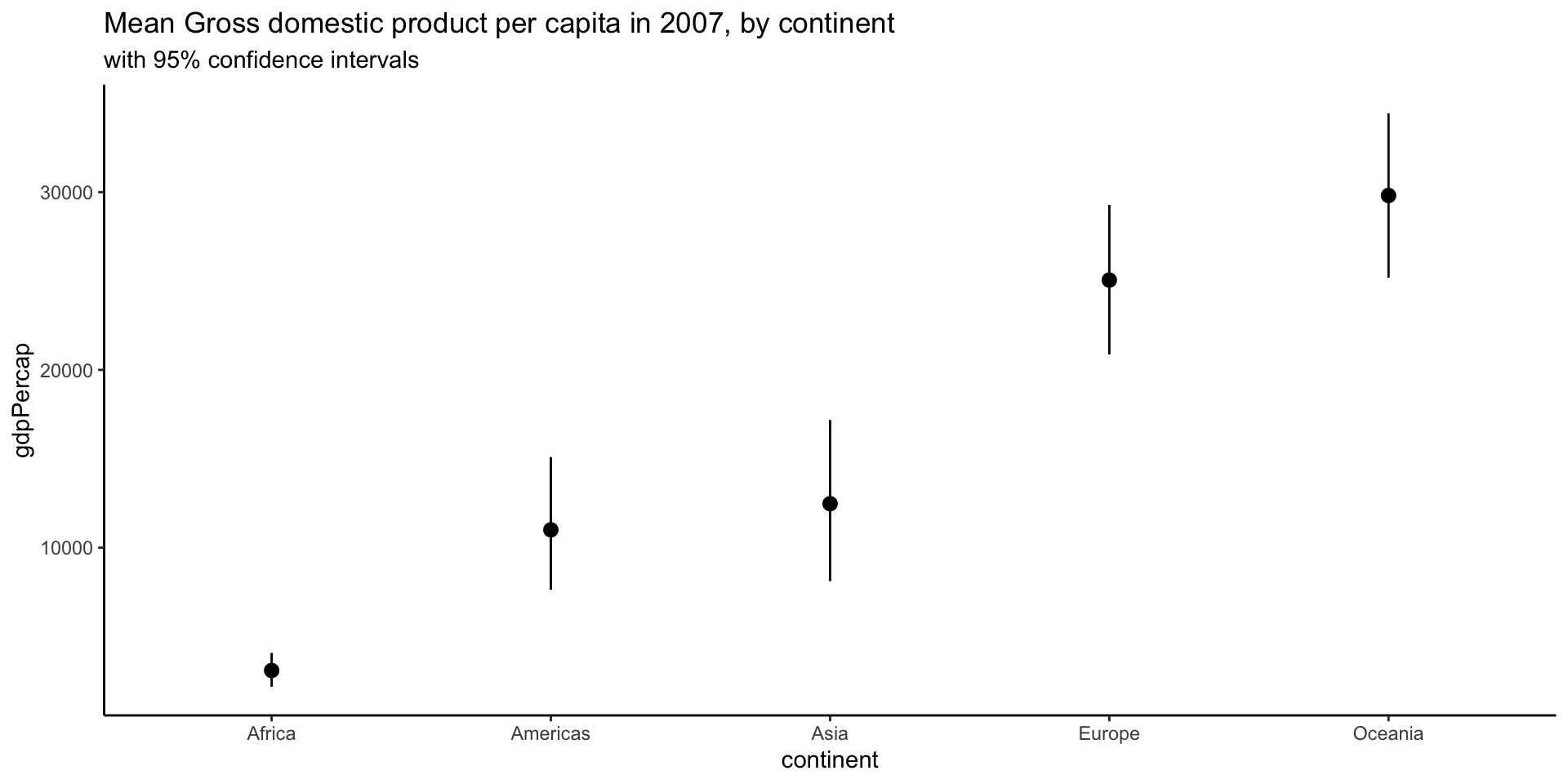
Comparing different experiments: pointrange with confidence intervals
Beware of pointranges!
What is the difference between these three plots? They are derived from the same data.
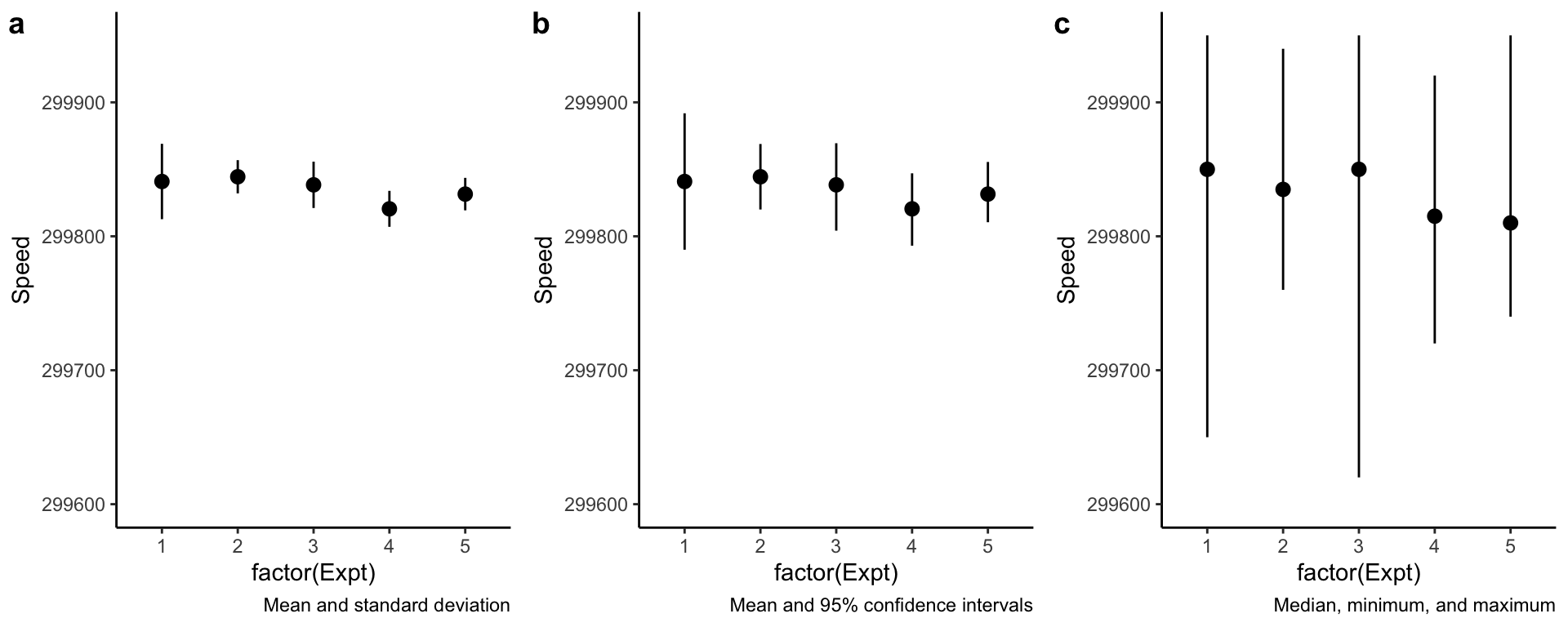
Beware of pointranges!
What is the difference between these three plots? They are derived from the same data.
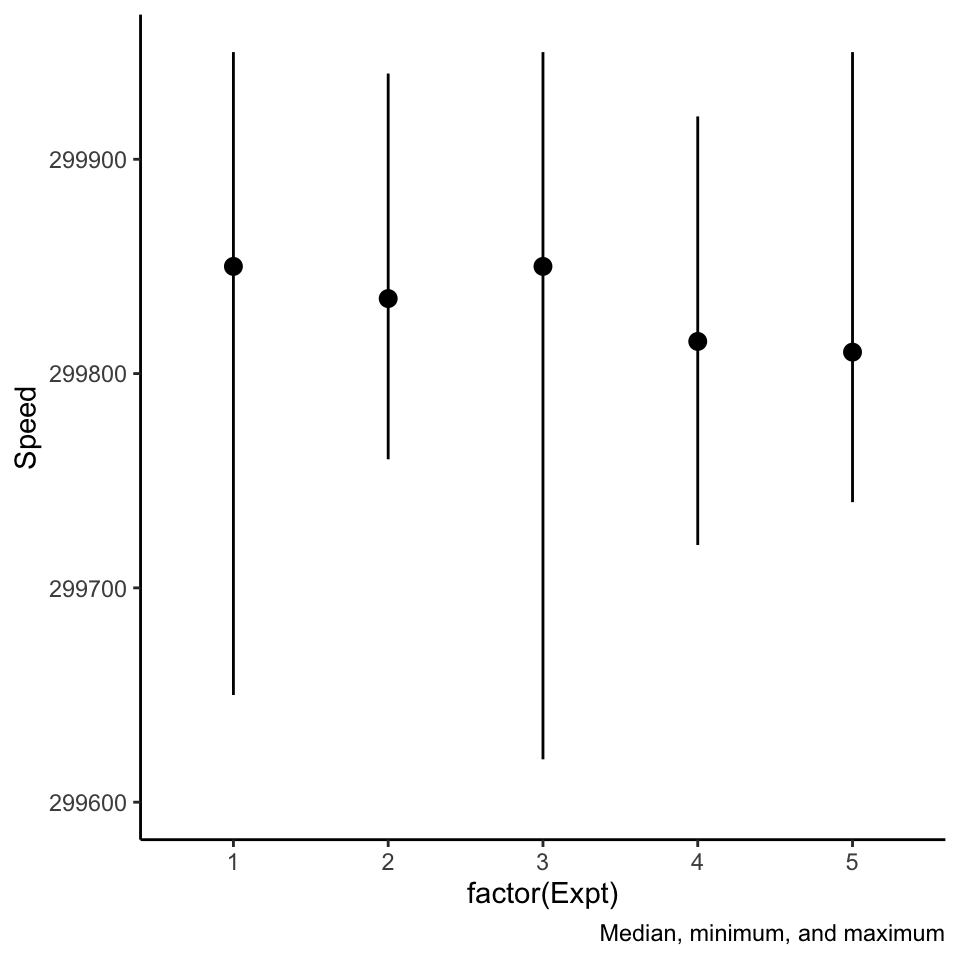
Beware of pointranges!
What is the difference between these three plots? They are derived from the same data.
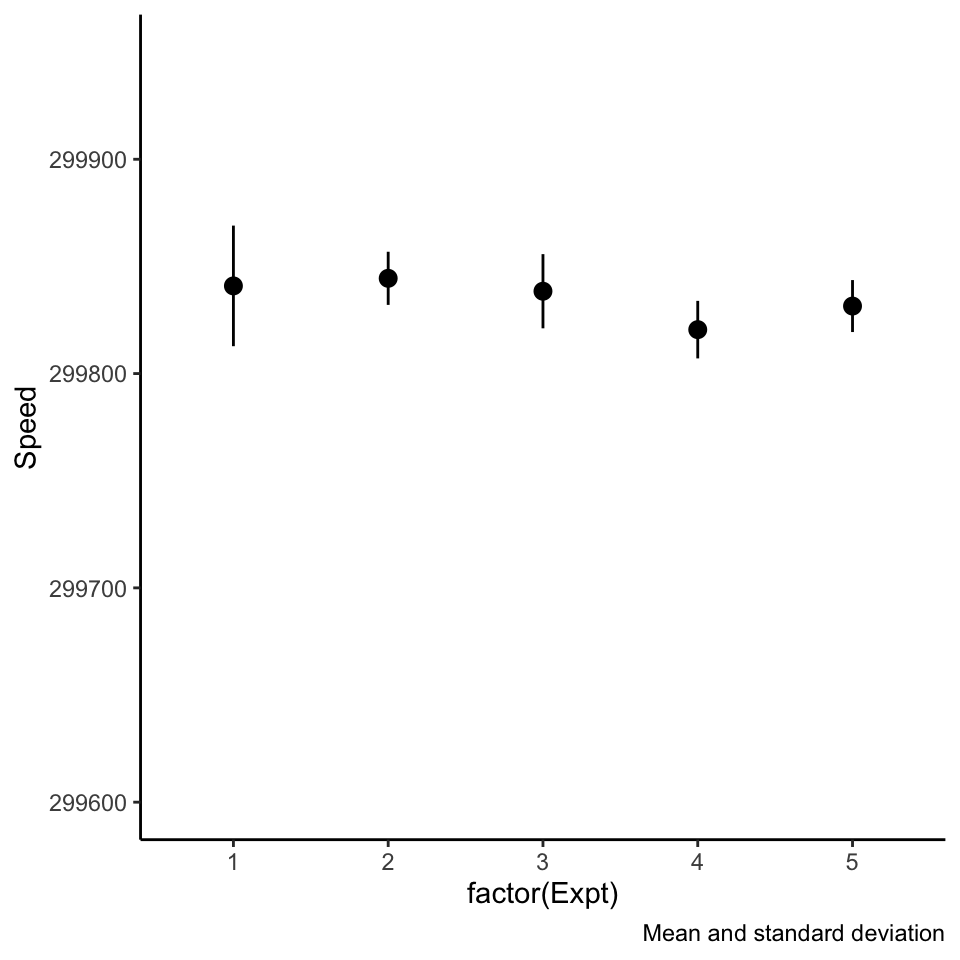
Beware of pointranges!
What is the difference between these three plots? They are derived from the same data.
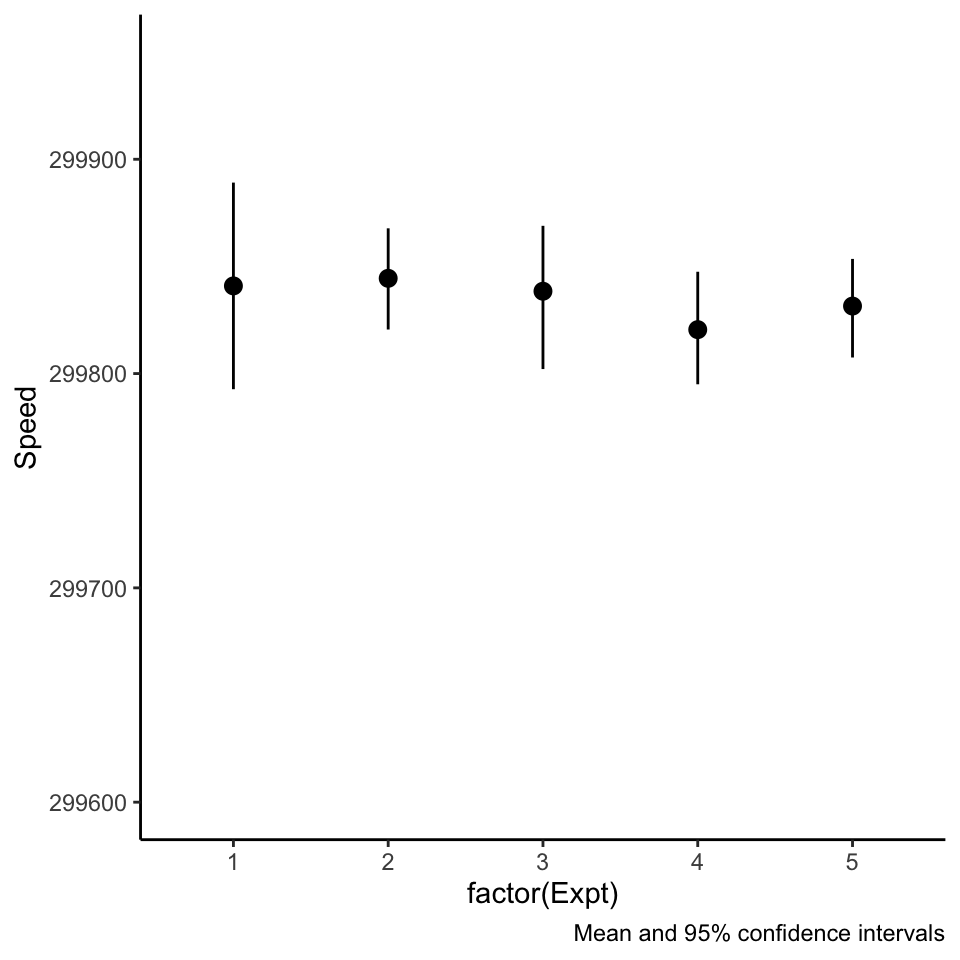
Beware of pointranges!
What is the difference between these three plots? They are derived from the same data.
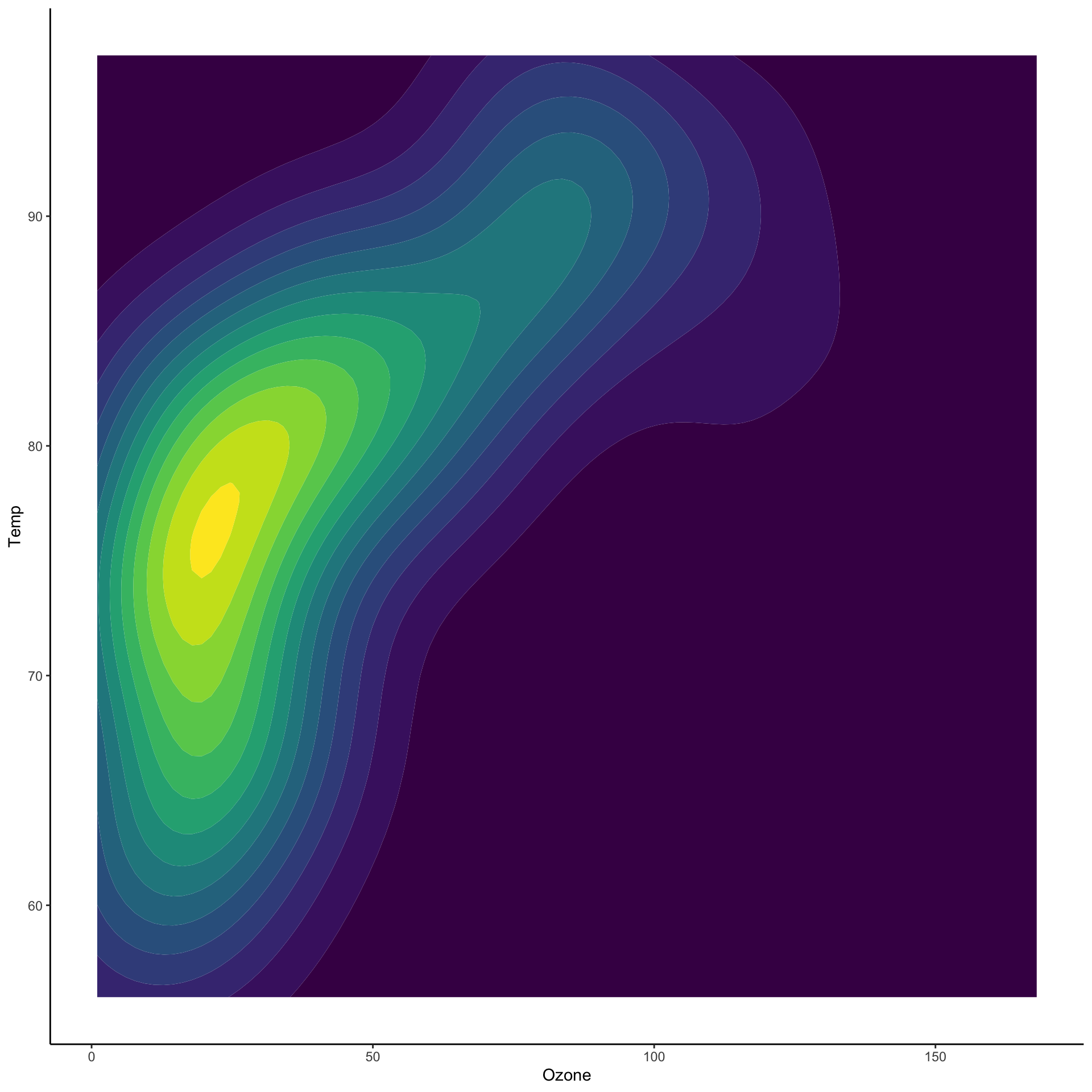
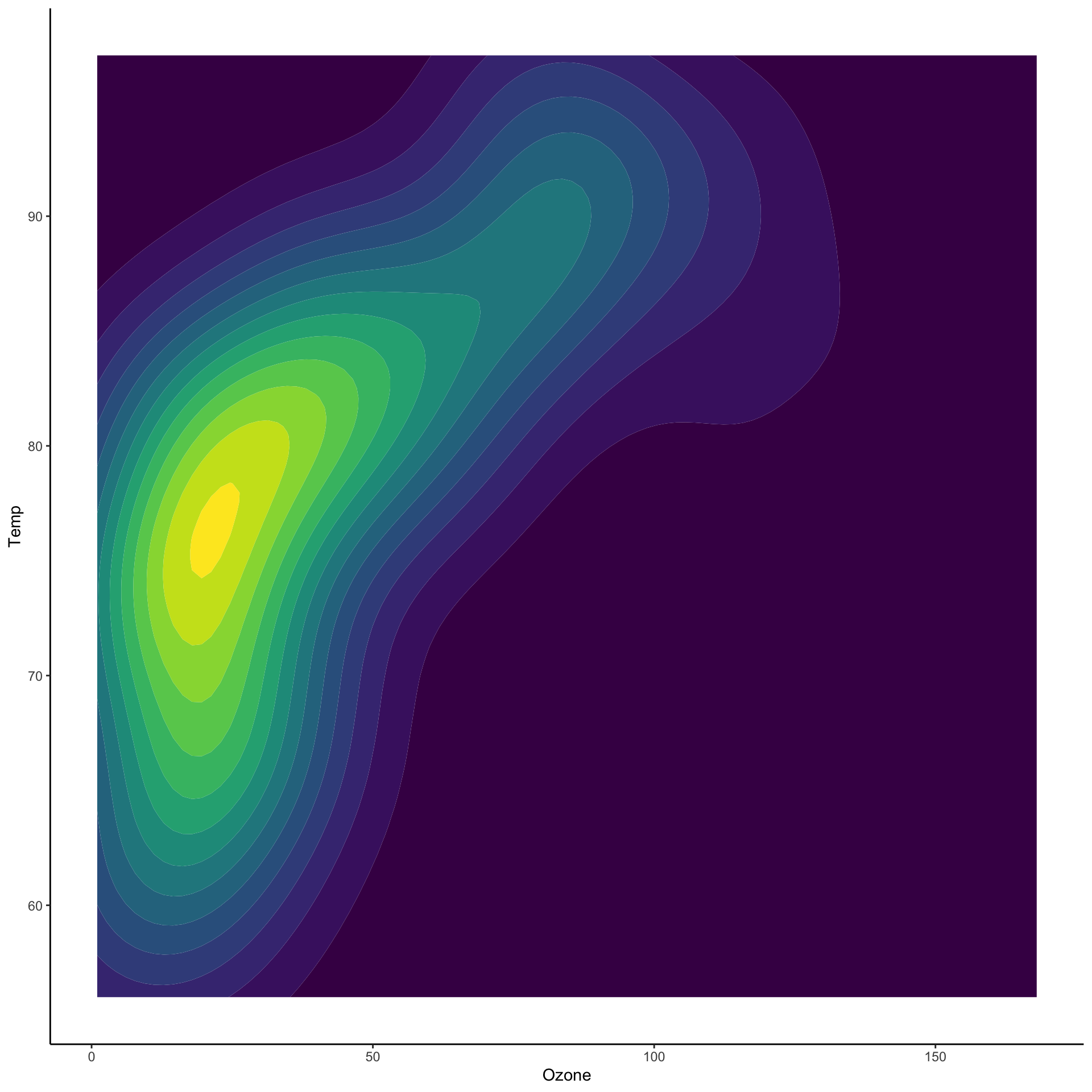
Two dimensional densities
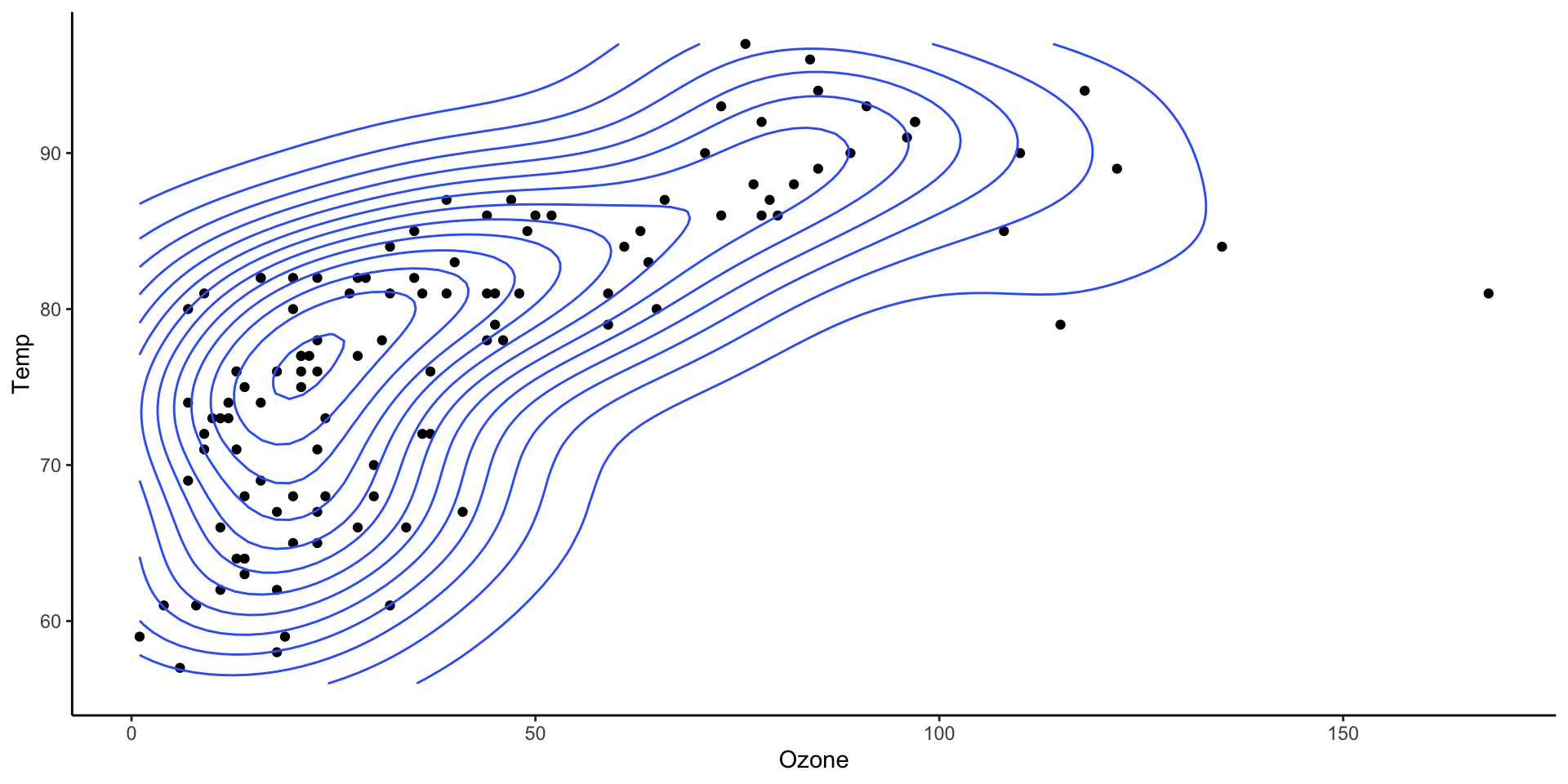
Two dimensional densities
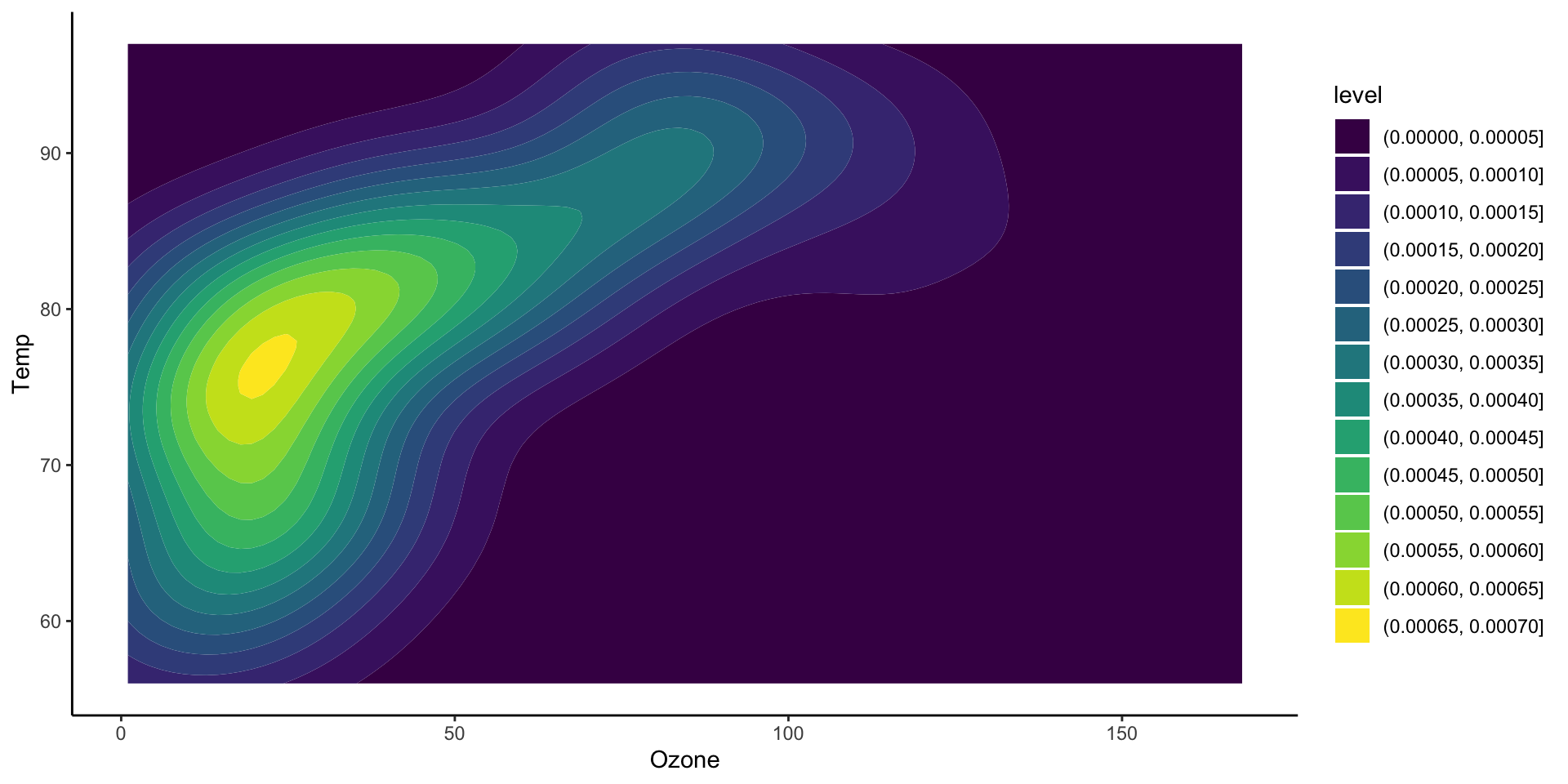
Two dimensional densities
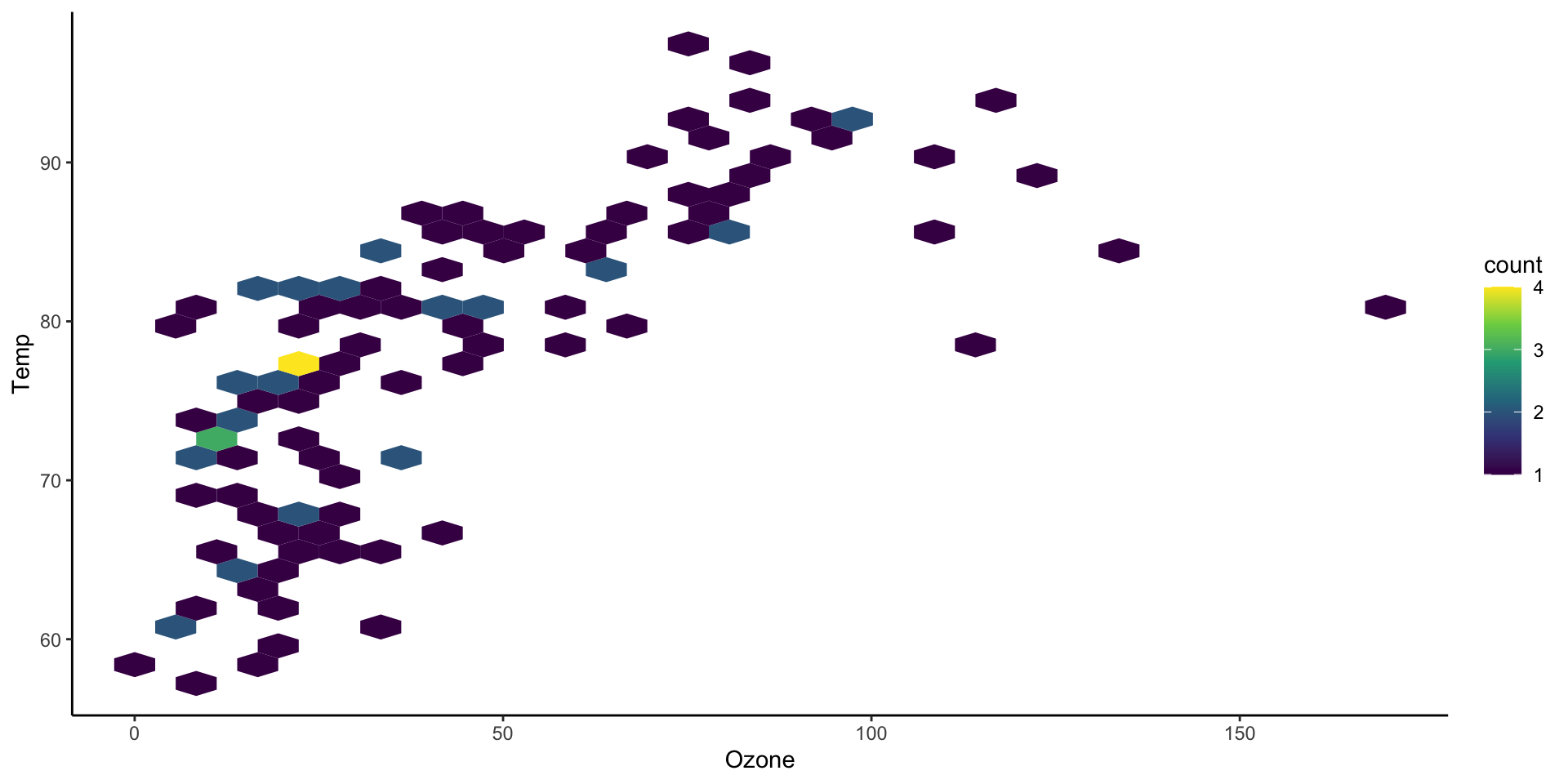
Two dimensional histograms
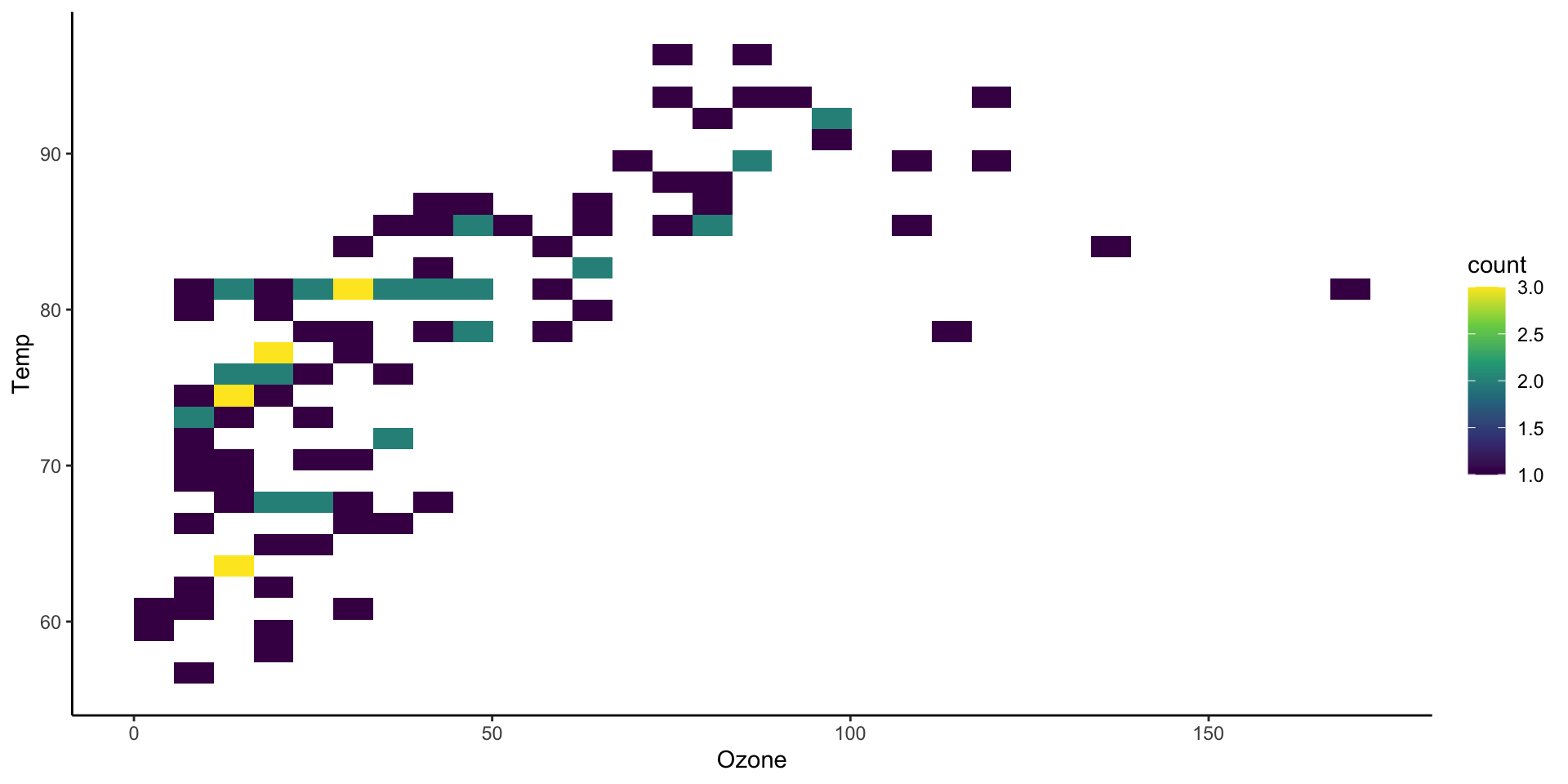
Two dimensional histograms
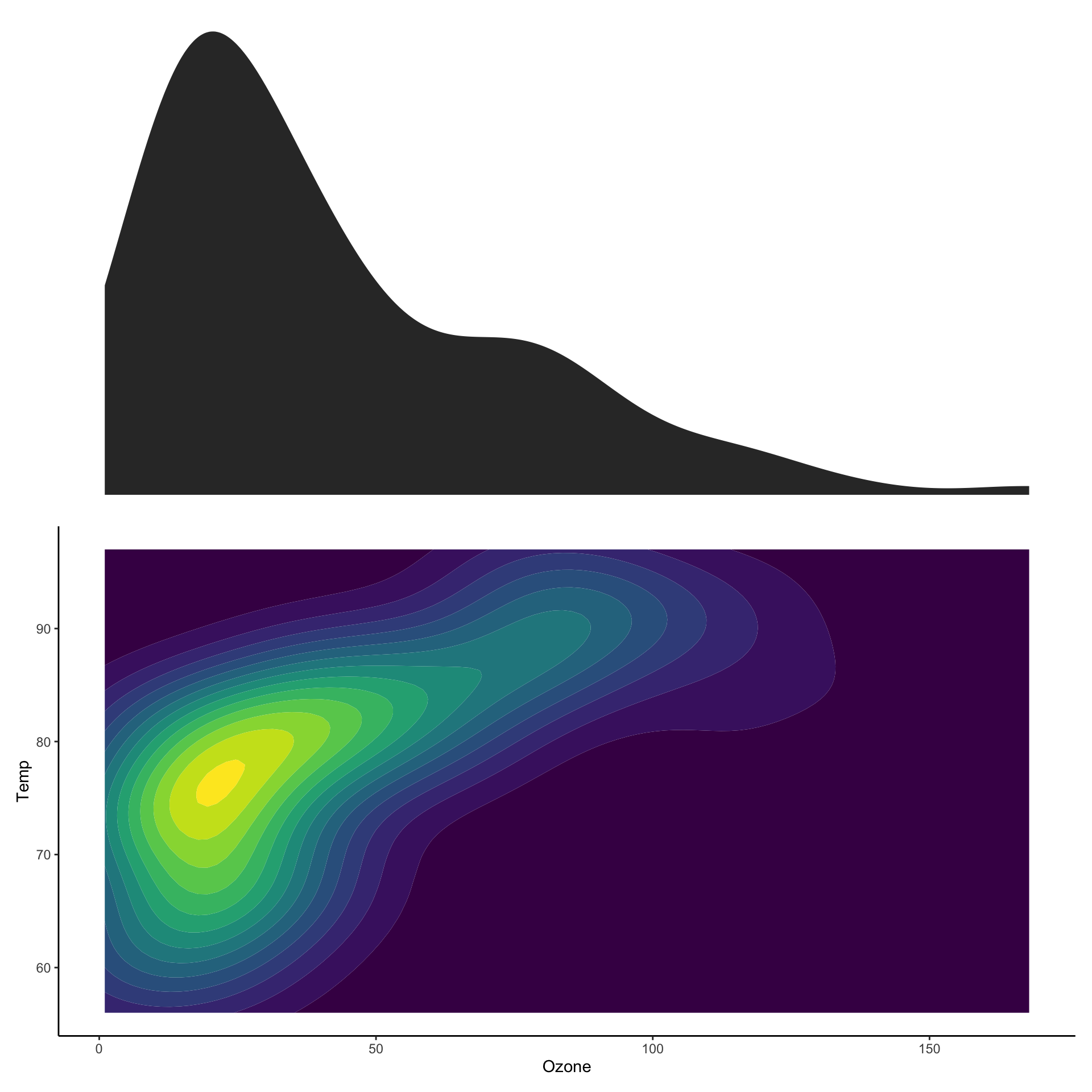
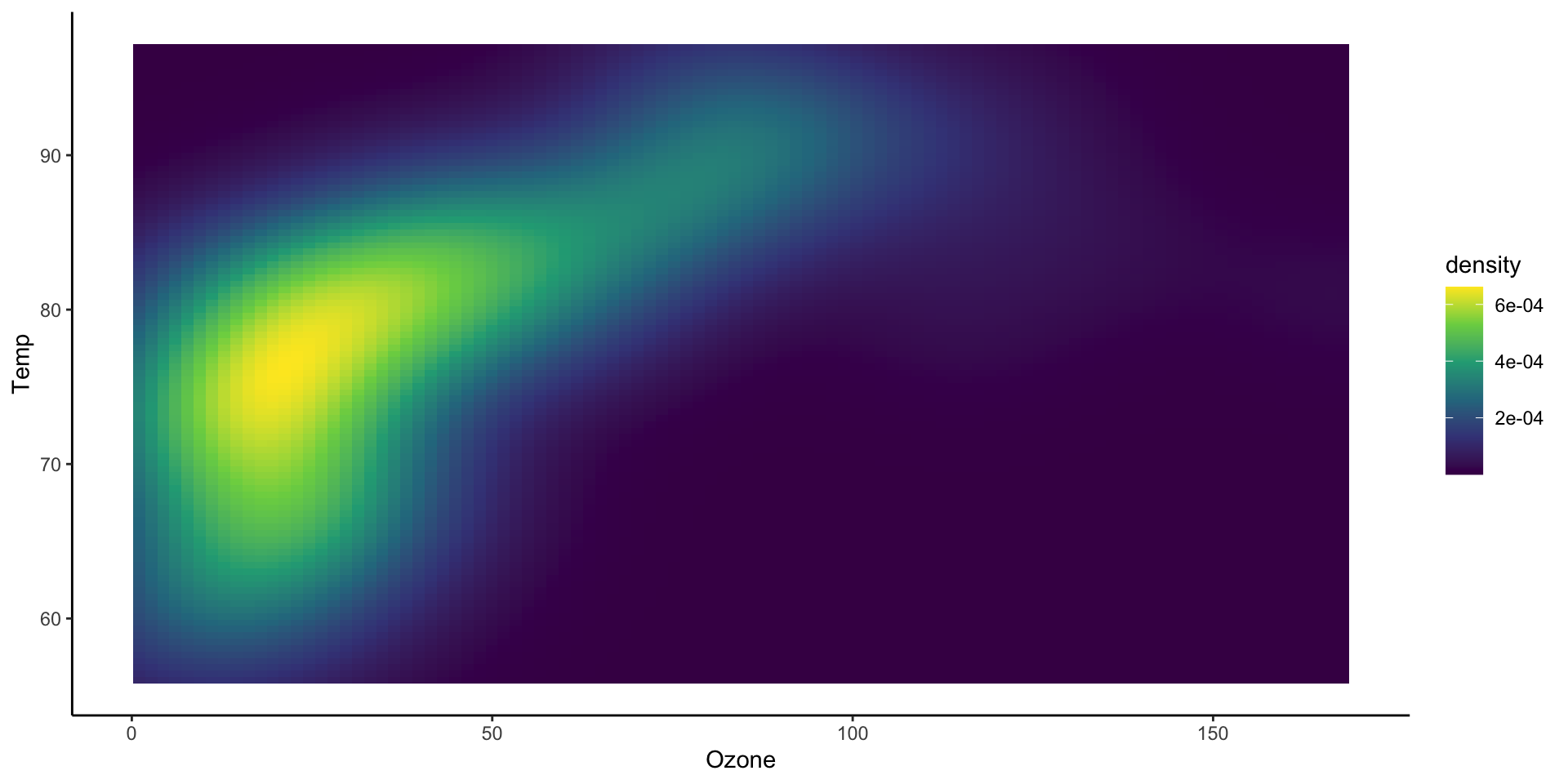
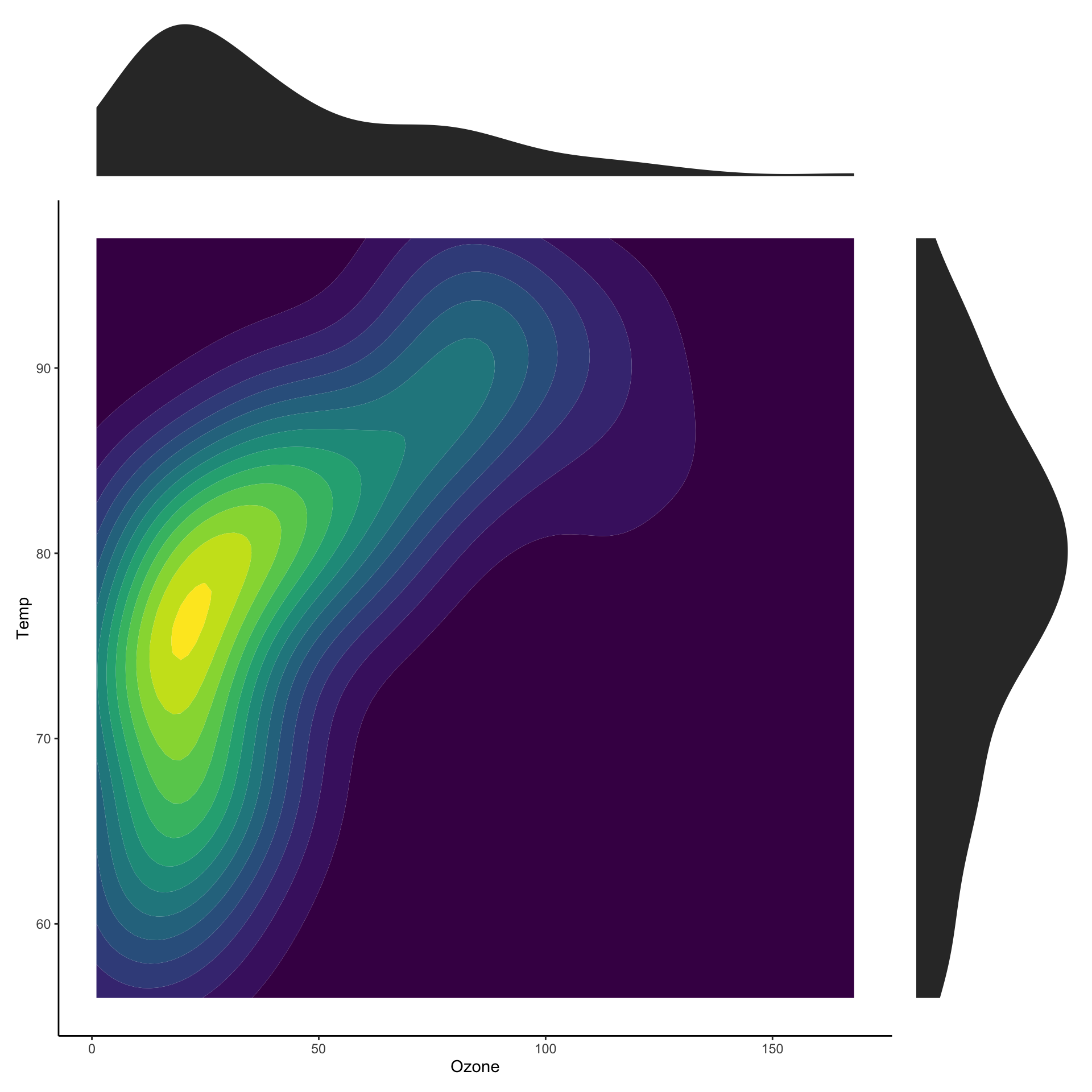
Showing marginal distributions
Showing marginal distributions
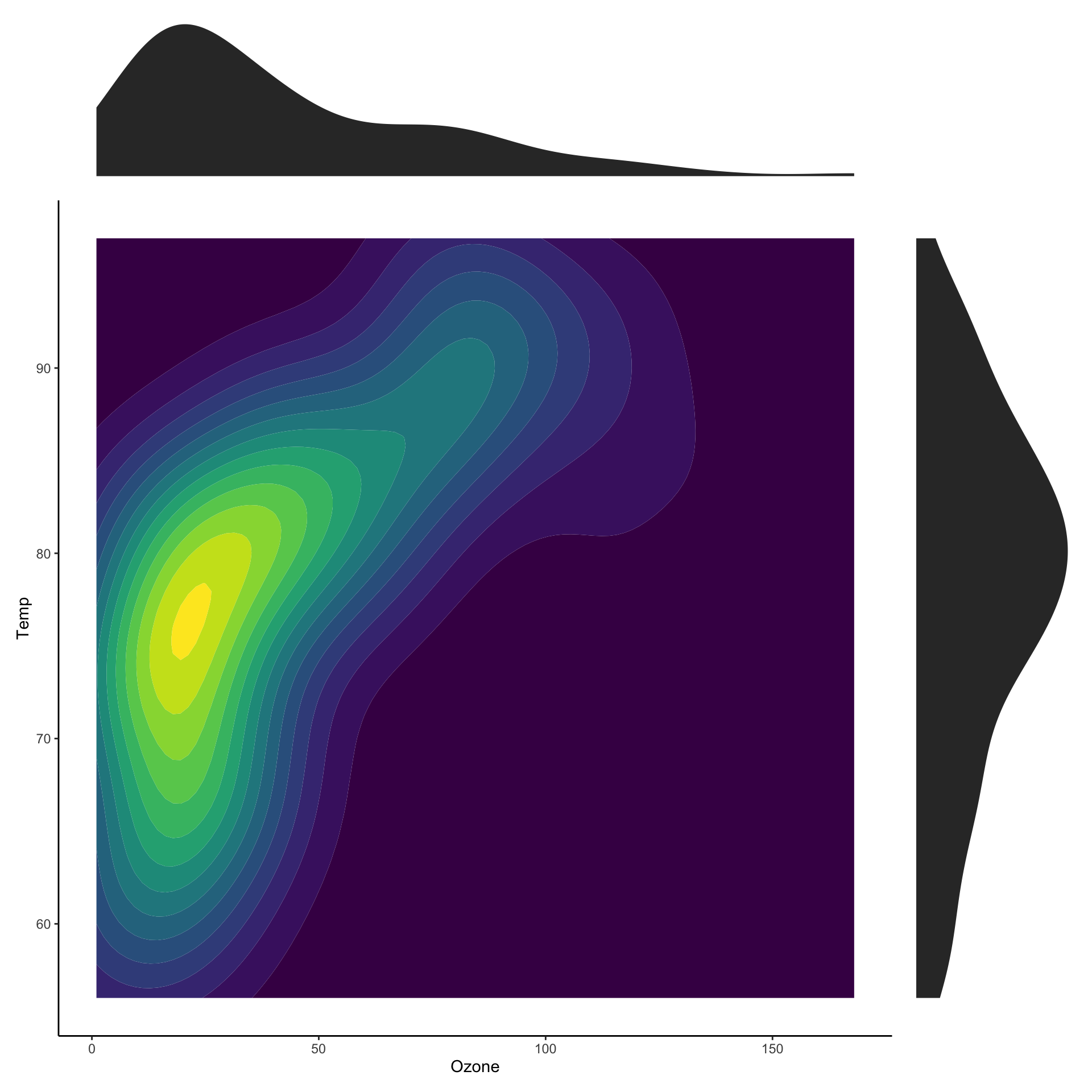
Showing marginal distributions
Showing marginal distributions
Showing marginal distributions
p_main <- ggplot(airquality,
aes(x=Ozone,
y=Temp)) +
stat_density2d_filled() +
theme(legend.position="none")
p_ozone <- ggplot(airquality, aes(x=Ozone)) +
stat_density() + theme_void()
p_temp <- ggplot(airquality, aes(x=Temp)) +
stat_density() + coord_flip() + theme_void()
wrap_plots(p_ozone, plot_spacer(),
p_main, p_temp,
nrow = 2
)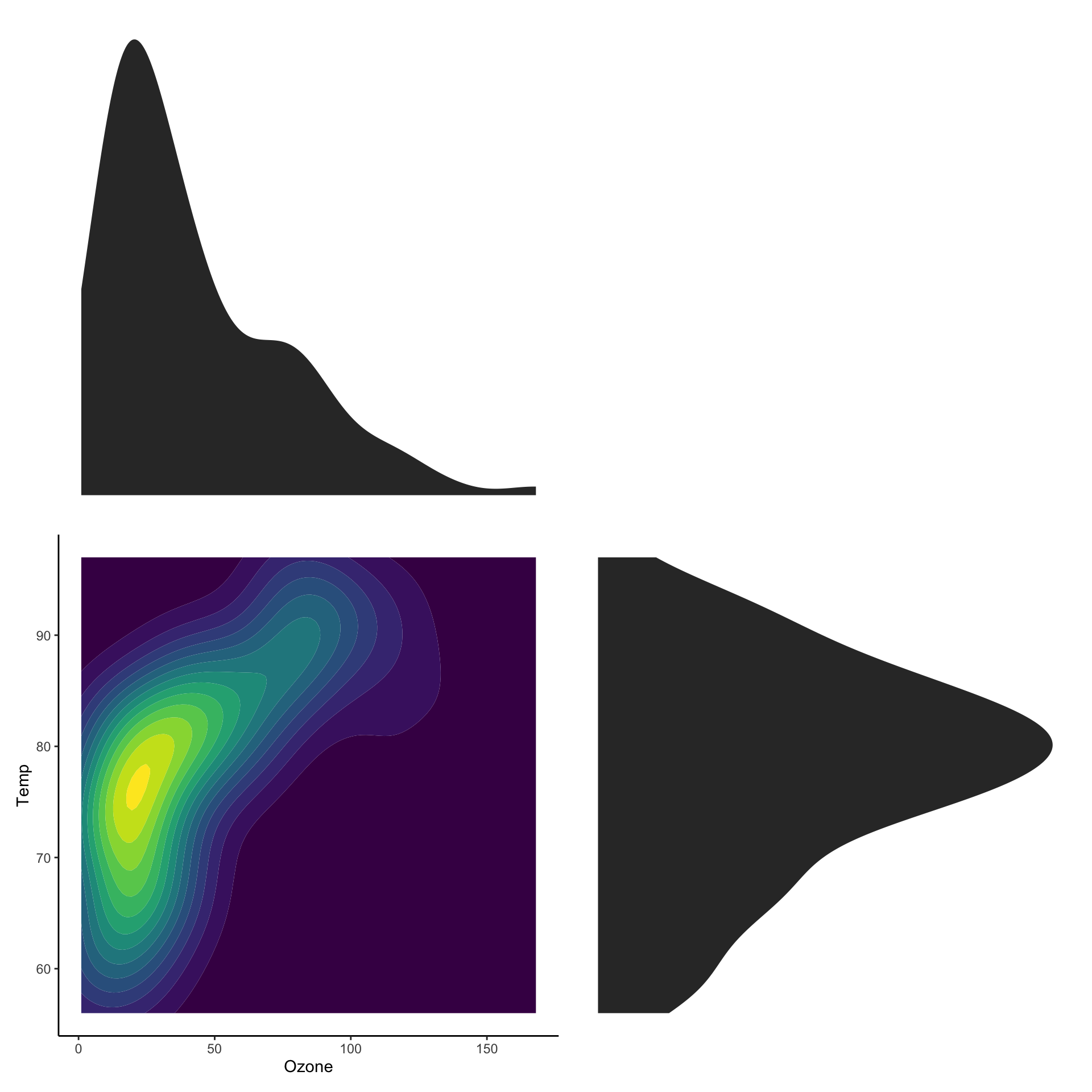
Showing marginal distributions
p_main <- ggplot(airquality,
aes(x=Ozone,
y=Temp)) +
stat_density2d_filled() +
theme(legend.position="none")
p_ozone <- ggplot(airquality, aes(x=Ozone)) +
stat_density() + theme_void()
p_temp <- ggplot(airquality, aes(x=Temp)) +
stat_density() + coord_flip() + theme_void()
wrap_plots(p_ozone, plot_spacer(),
p_main, p_temp,
nrow = 2,
widths = c(1, 0.2),
heights = c(0.2, 1)
)
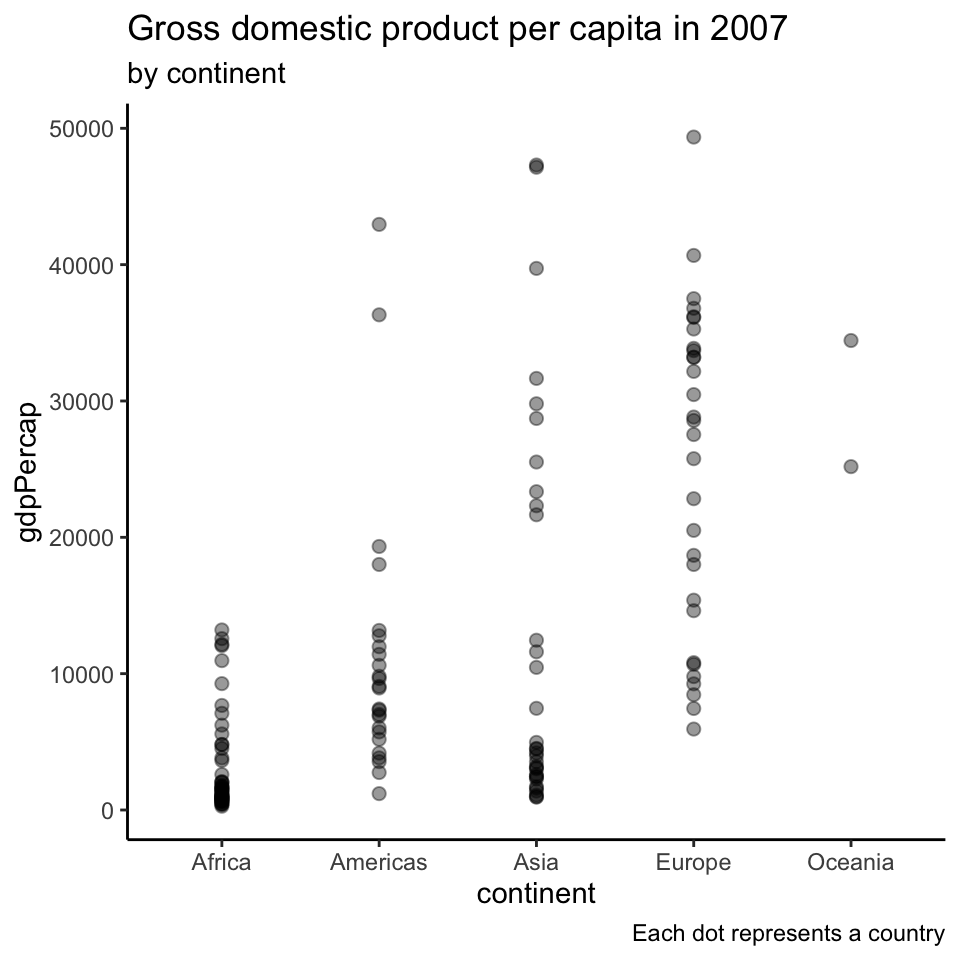
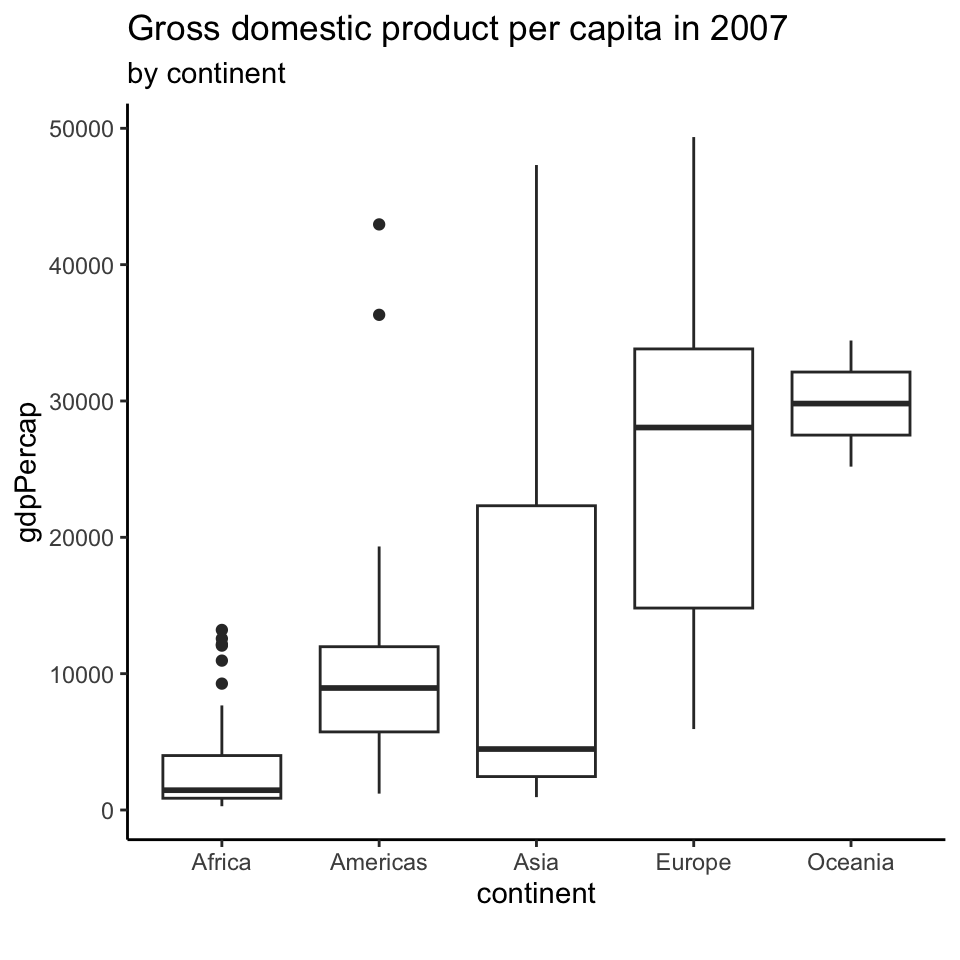
Representing large sets of values
Does this plot make sense?
We are modelling countries as realizations of a random sample.
Showing all the data points
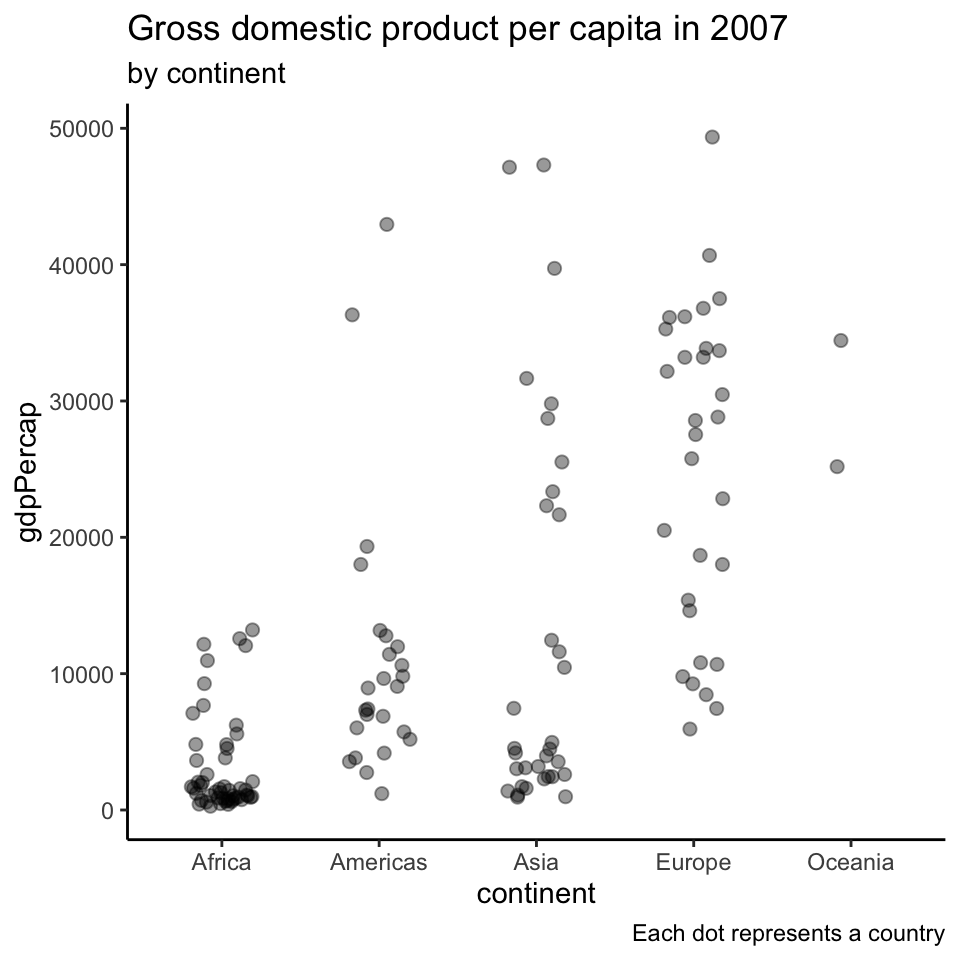
Showing all the data points (2)
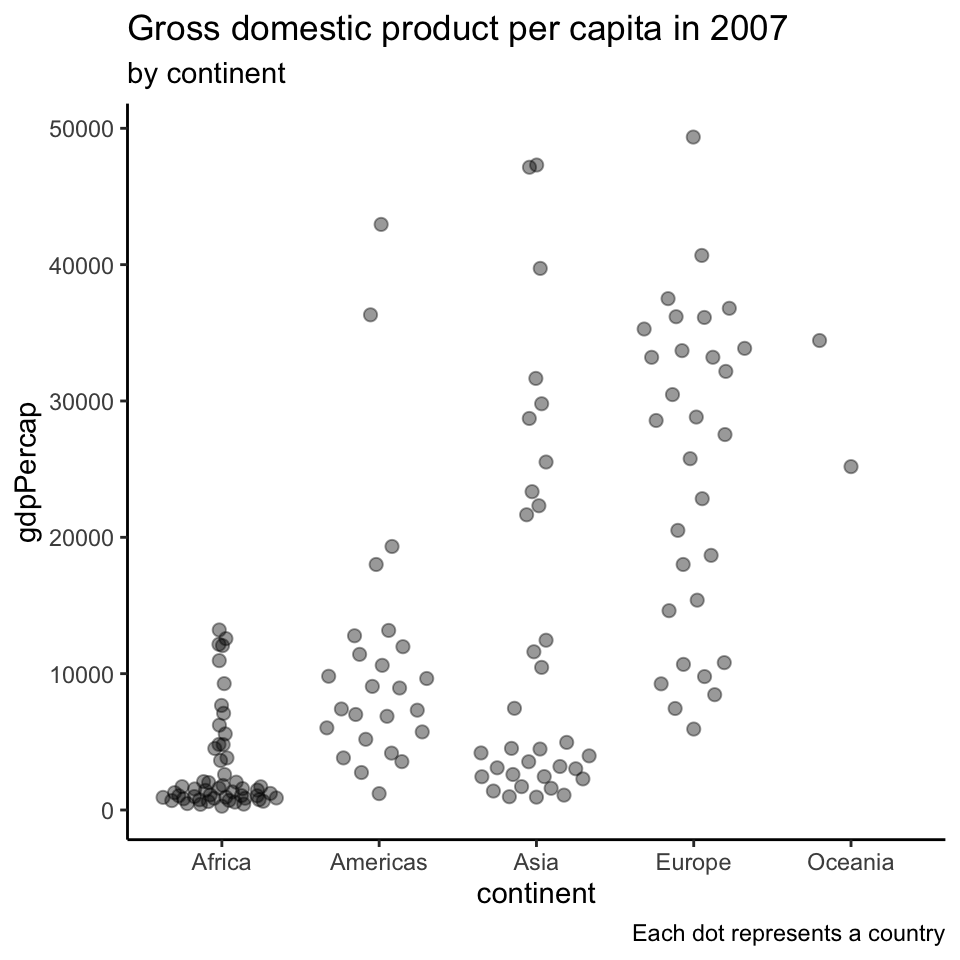
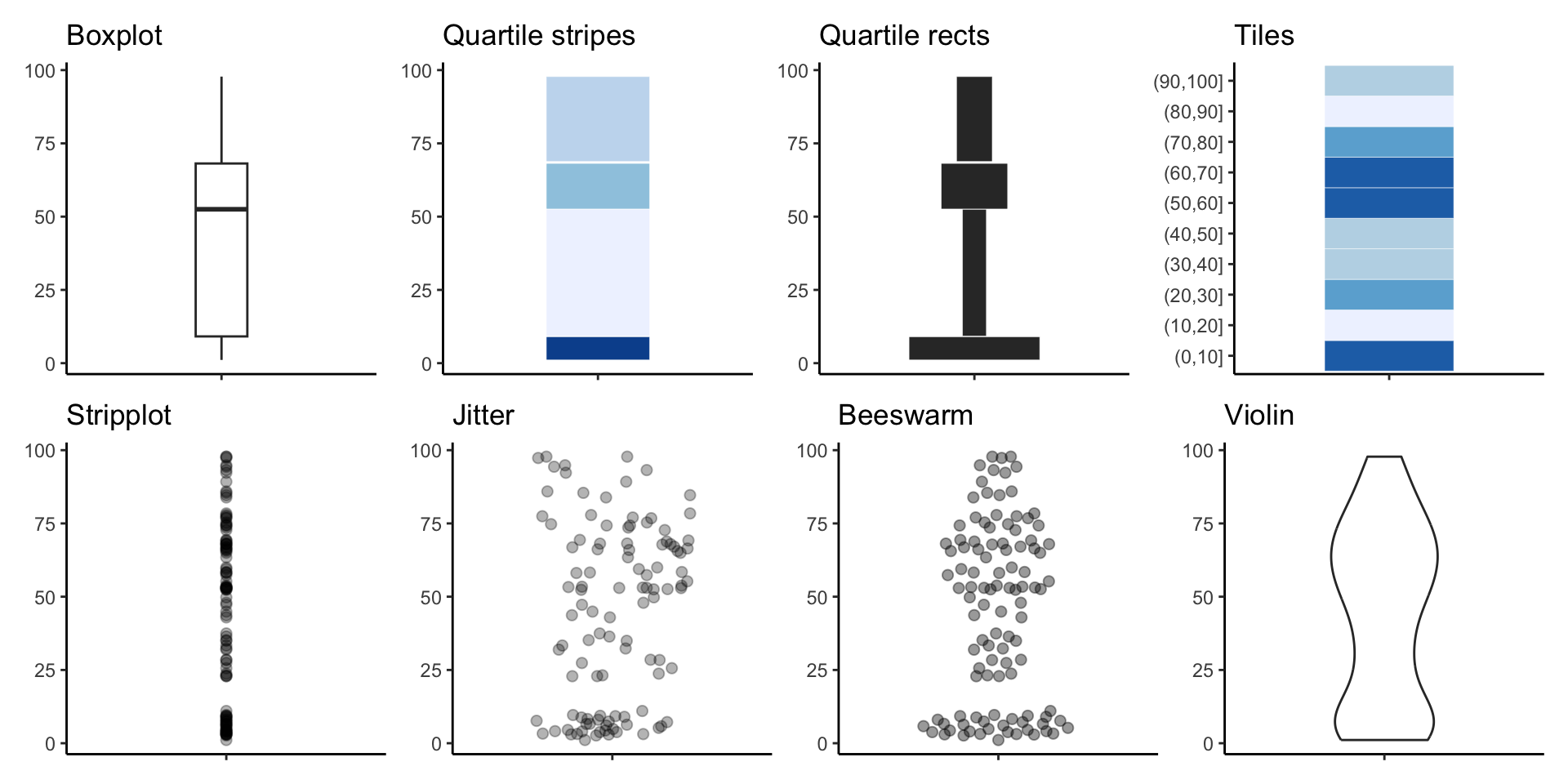
Beeswarm
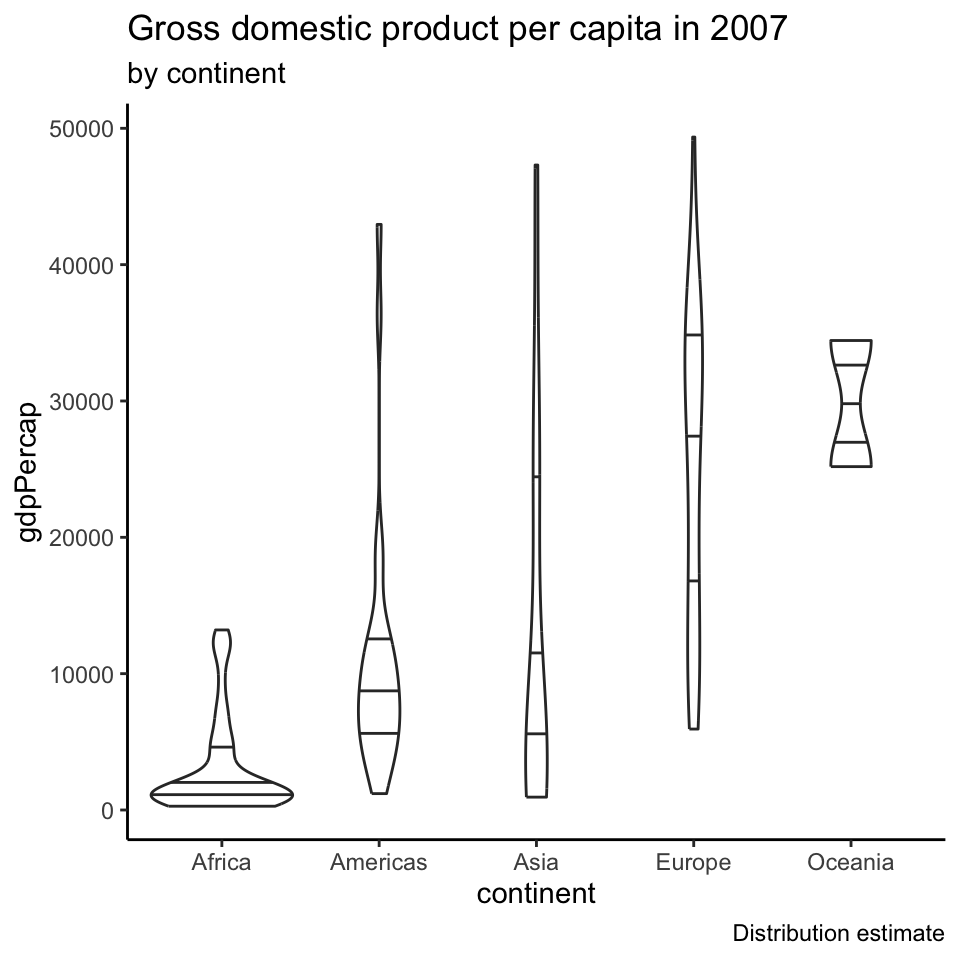
Violin plots
Using quantiles to summarize a dataset
These 5 numbers nicely summarize a dataset
- mimum
- \(0.25\)-quantile
- median
- \(0.75\)-quantile
- maximum
The Inter Quantile Range (IQR) is the data interval between \(q(0.75)\) and \(q(0.25)\)
It tells you the range where the “middle half” of the dataset is.
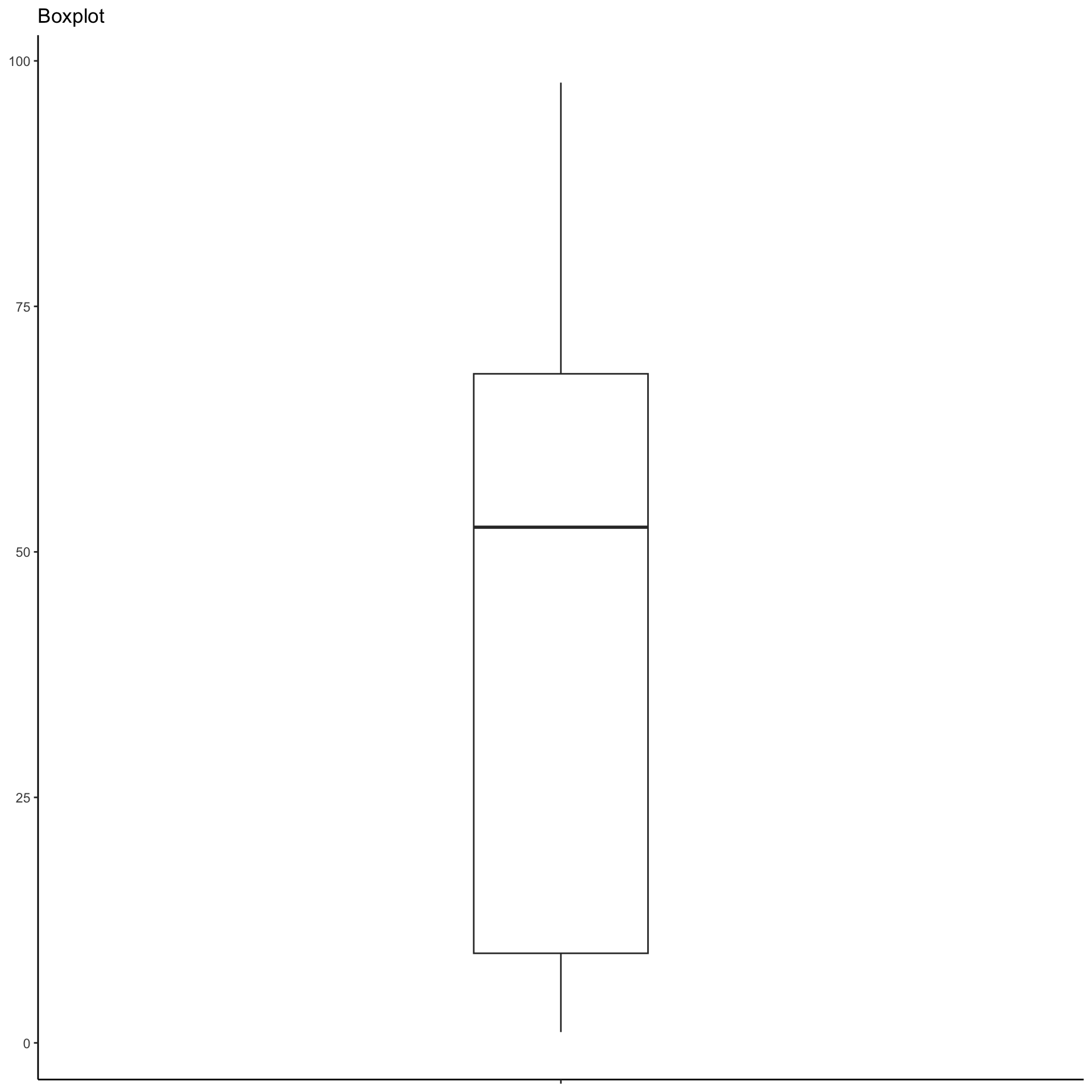
Box plots
Box plots (2)
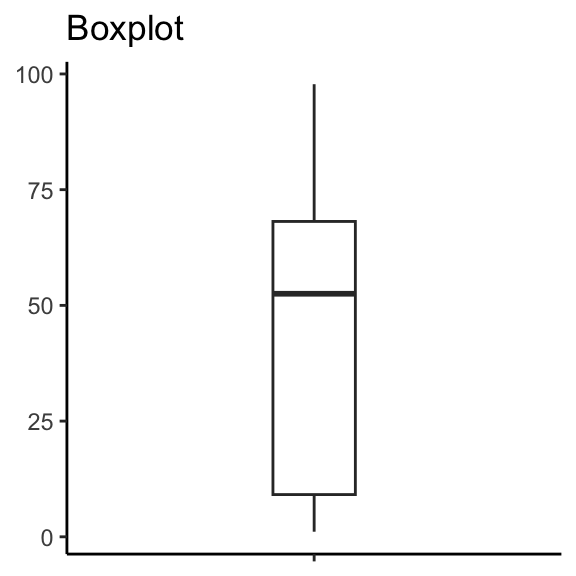
Box plots (2)
How many points are there between 0 and 10?
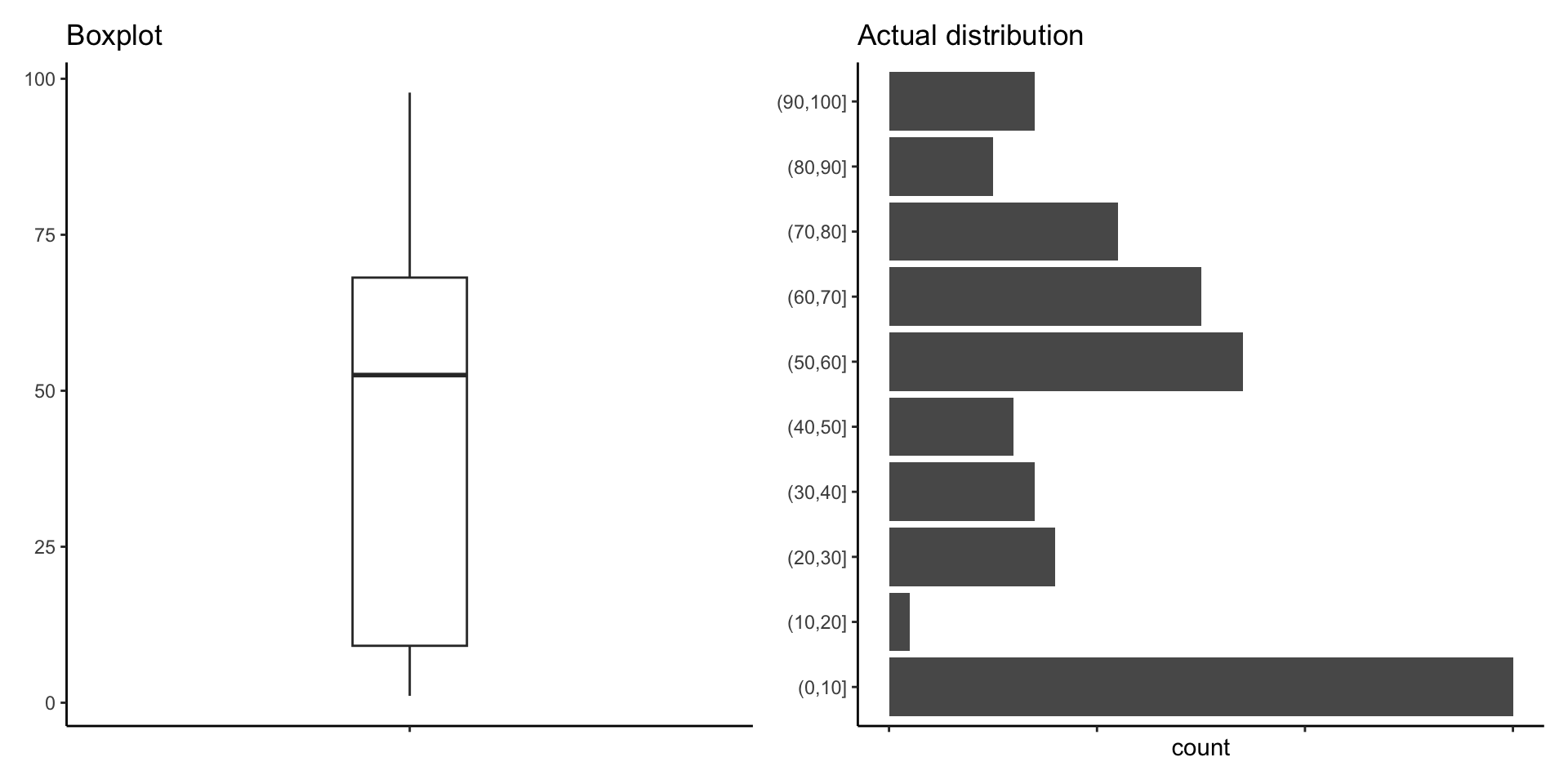
Box plots (2)
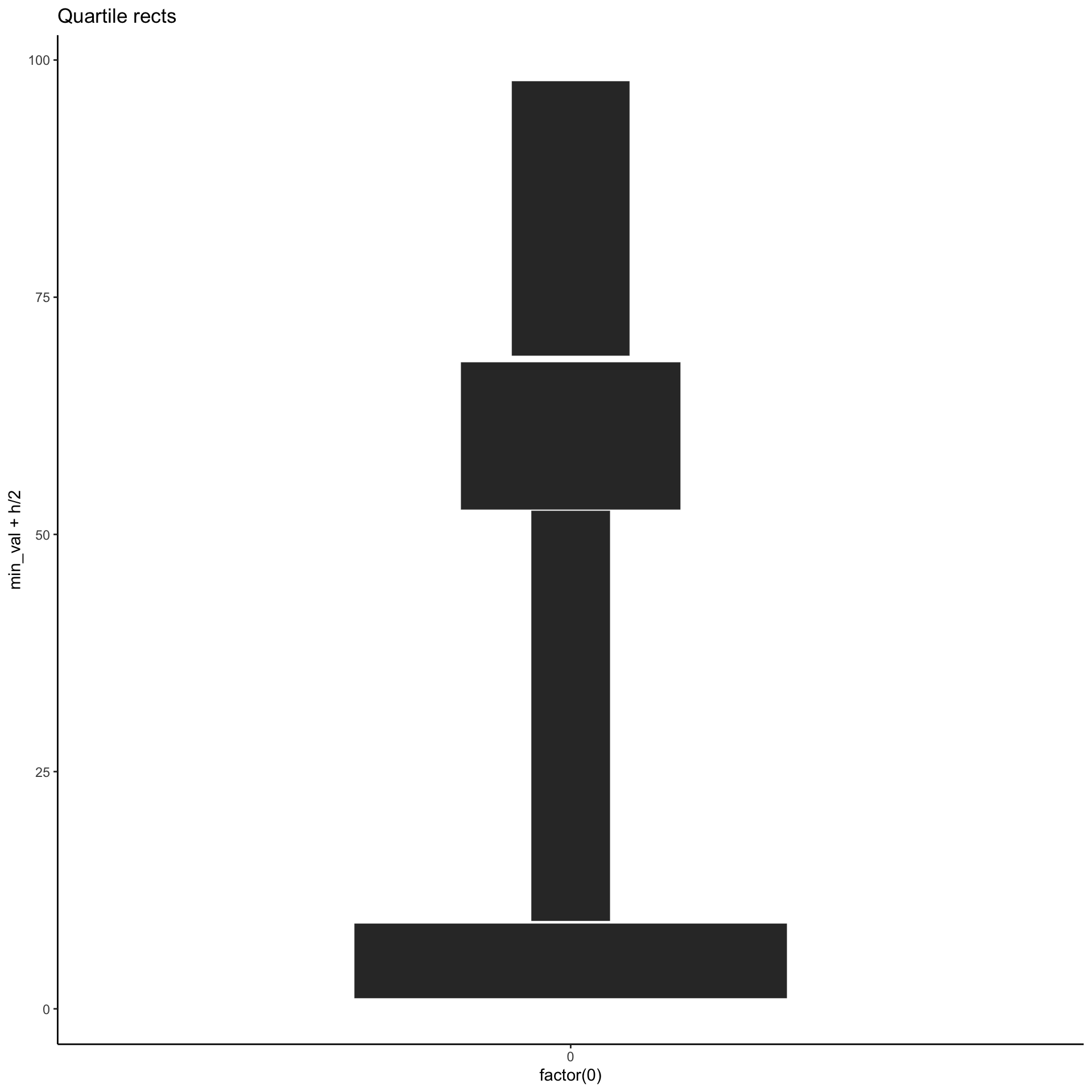
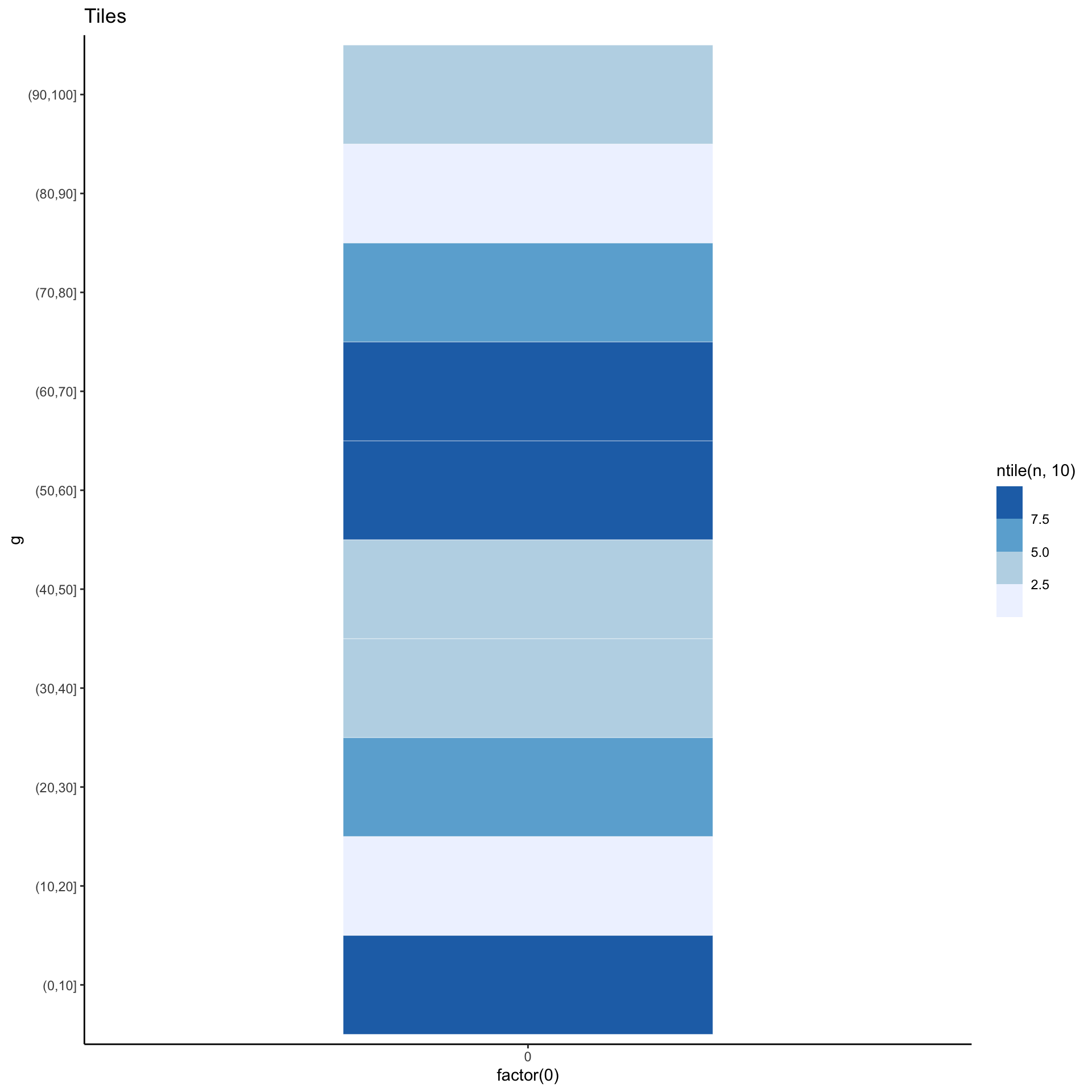
A potential alternative
A potential alternative
A potential alternative
A potential alternative
# A tibble: 4 × 5
g min_val max_val h w
<int> <dbl> <dbl> <dbl> <dbl>
1 1 1.10 9.00 7.90 0.506
2 2 9.25 52.5 43.3 0.0925
3 3 52.6 68.2 15.6 0.257
4 4 68.8 97.8 29.0 0.138 A potential alternative
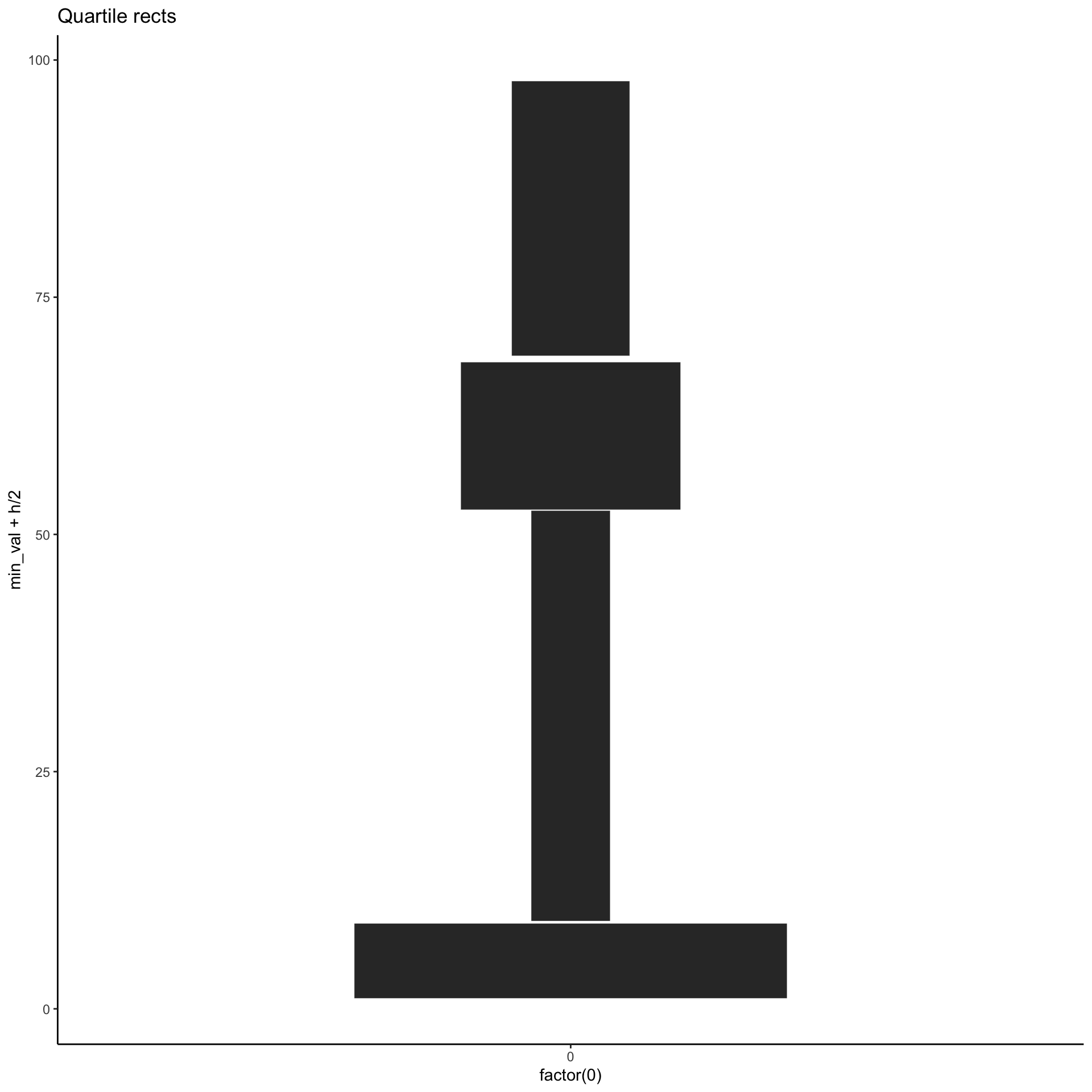
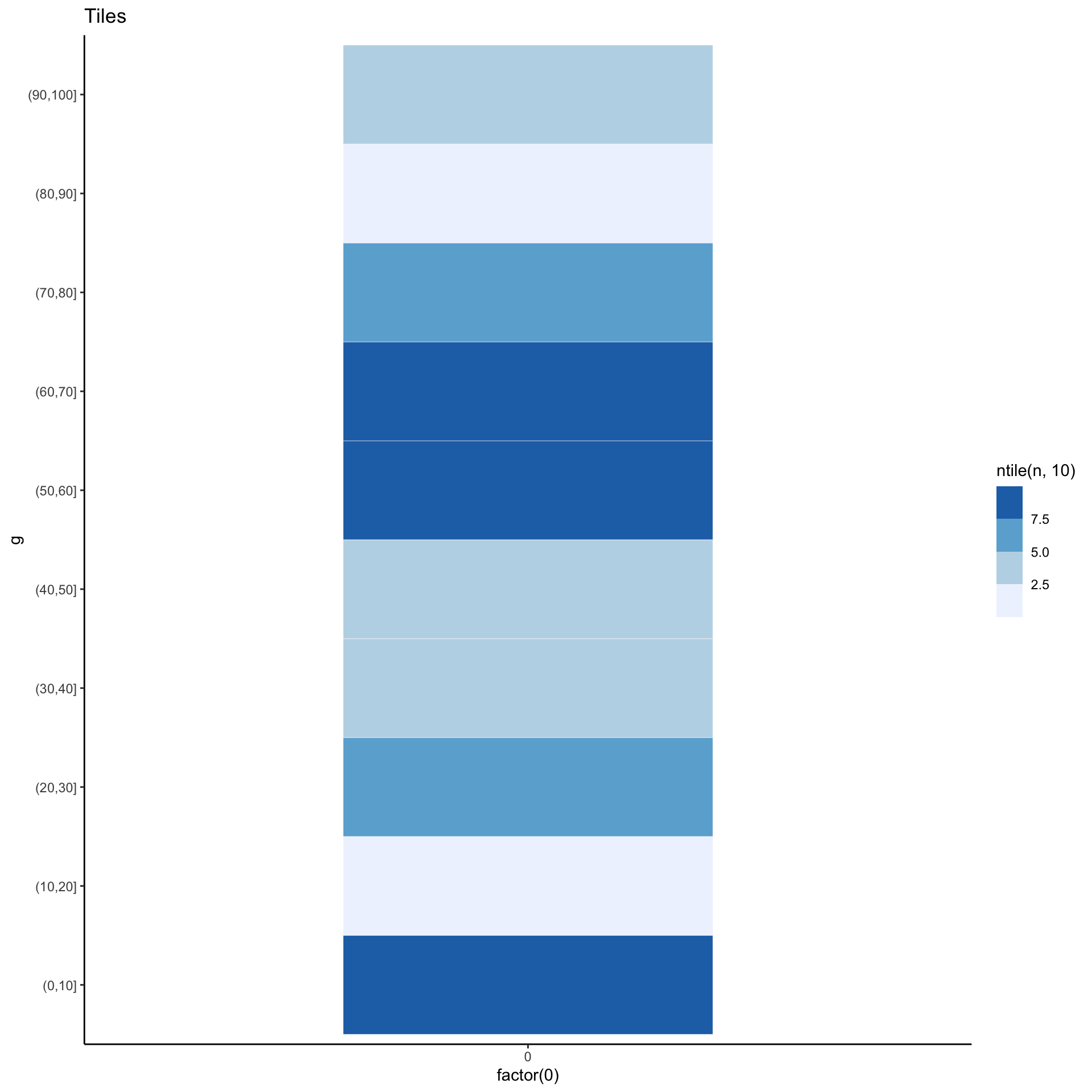
Another alternative
p_stripes <- unbalanced %>%
group_by(
g = ntile(val, 4)
) %>%
summarise(
min_val = min(val),
max_val = max(val),
h = max_val - min_val,
w = 4/h
) %>%
ggplot(aes(x = factor(0),
y=min_val + h/2,
height = h,
fill = w)) +
labs(title="Quartile stripes") +
geom_tile(width = 0.4, color="white") +
scale_fill_fermenter(direction = 1)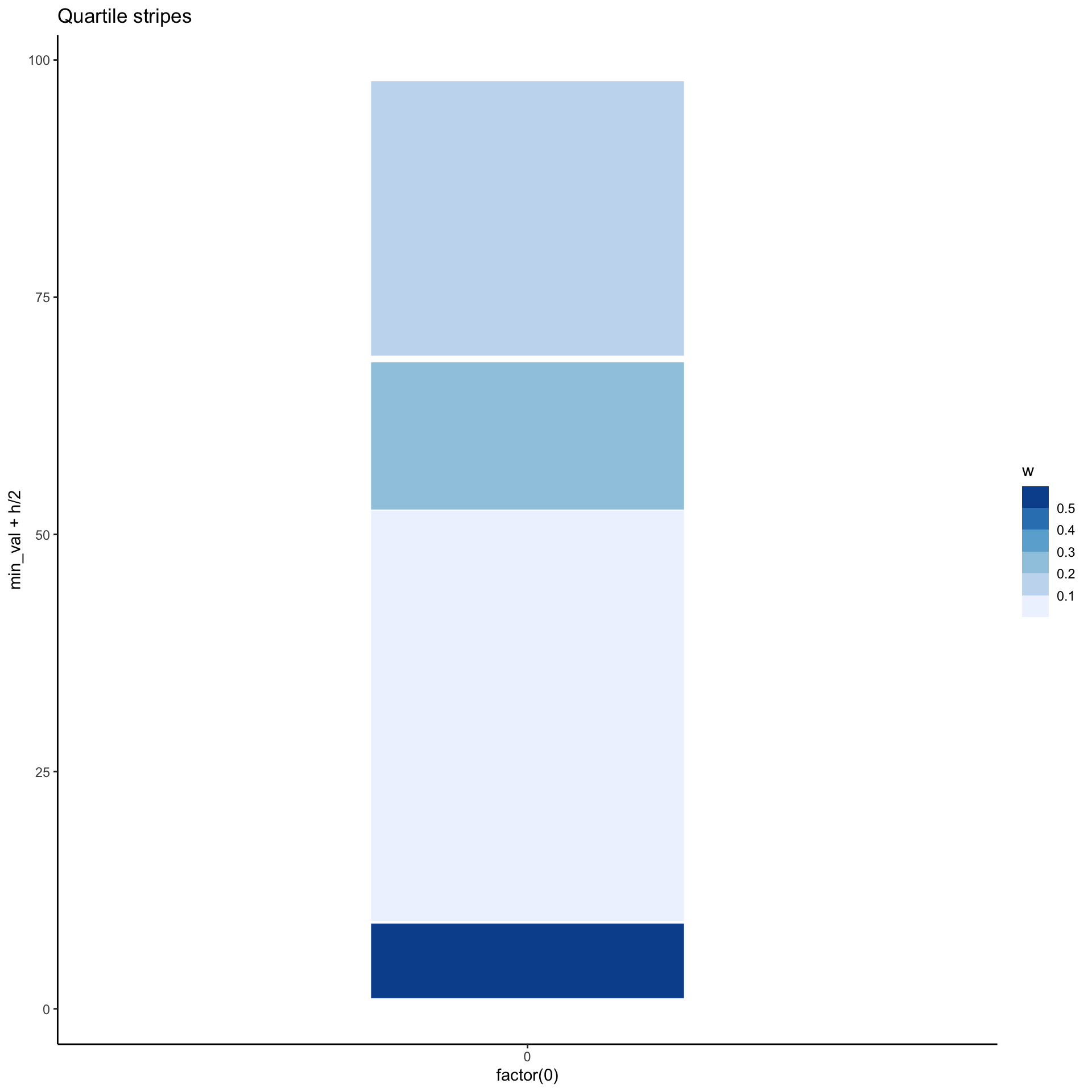
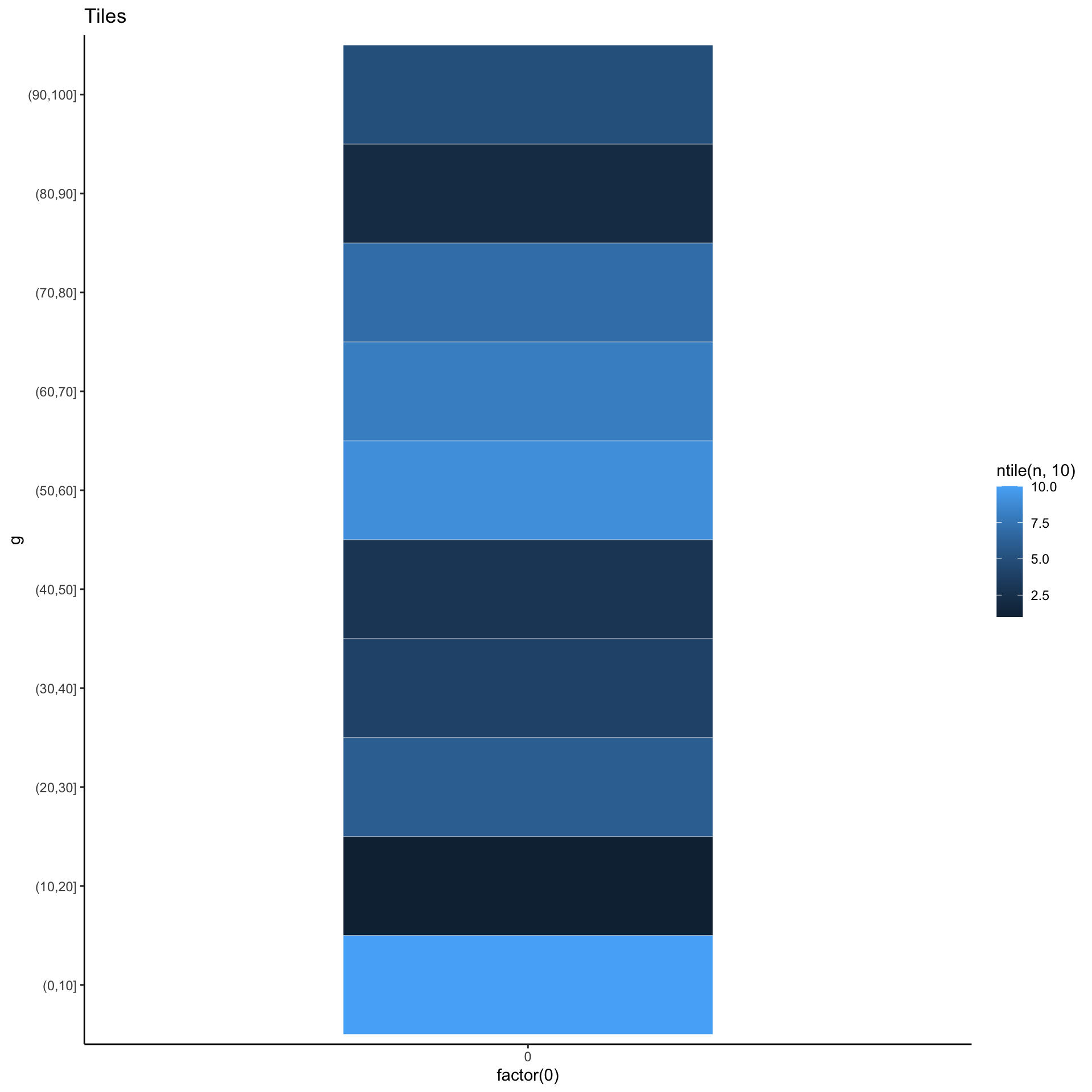
Yet another alternative
Yet another alternative
Yet another alternative
Yet another alternative
Yet another alternative
All together now!
Data Visualization and Exploration - Representing Uncertainty - ozan-k.com