Introduction to R

Data Visualization and Exploration

Ozan Kahramanoğulları

The R programming language

R is a language and environment for statistical computing and graphics.

You will use it both for this course and for the Mathematics and Statistics course.

R: language overview

Some fundamental features

Interacting with the console

Interacting with the console

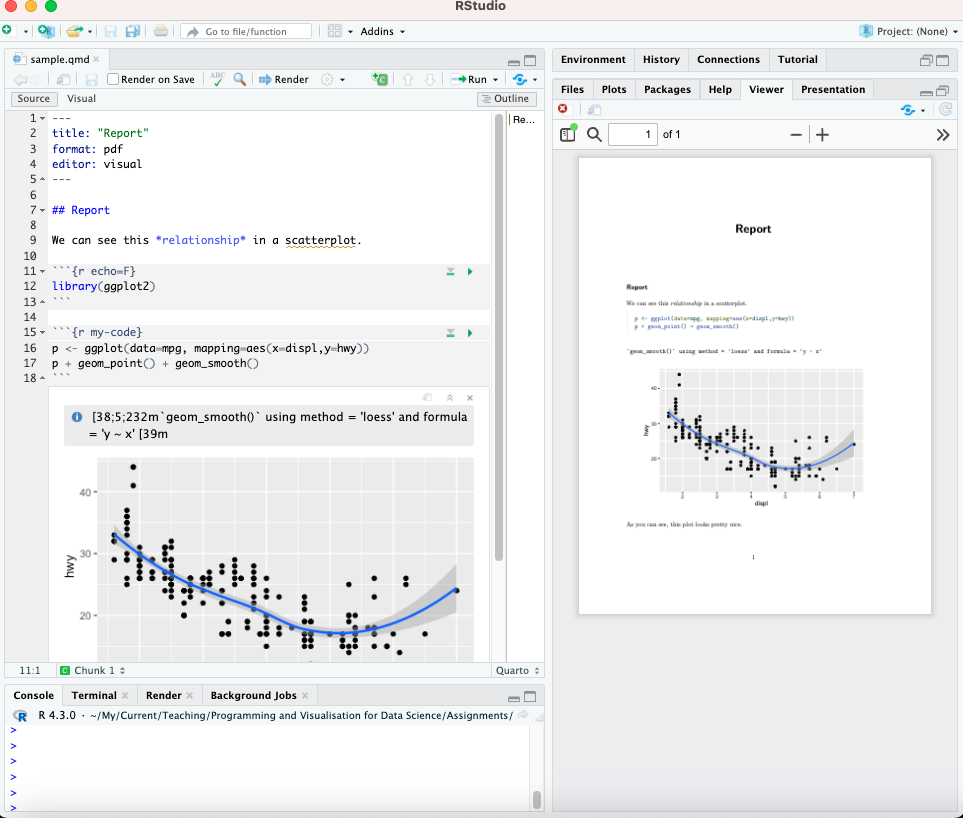
RMarkdown

RMarkdown is a plain text format (and accompanying tools) that allows you to intersperse text, code, and outputs.

obsolete

replaced with Quarto

(RMarkdown is integrated into Quarto)

The RMarkdown pipeline

Advantages of RMarkdown Quarto

  • Keep analysis code together with discussion conclusions

  • Easily keep everything under version control

  • Reproducibility

  • Similar to Python’s notebooks

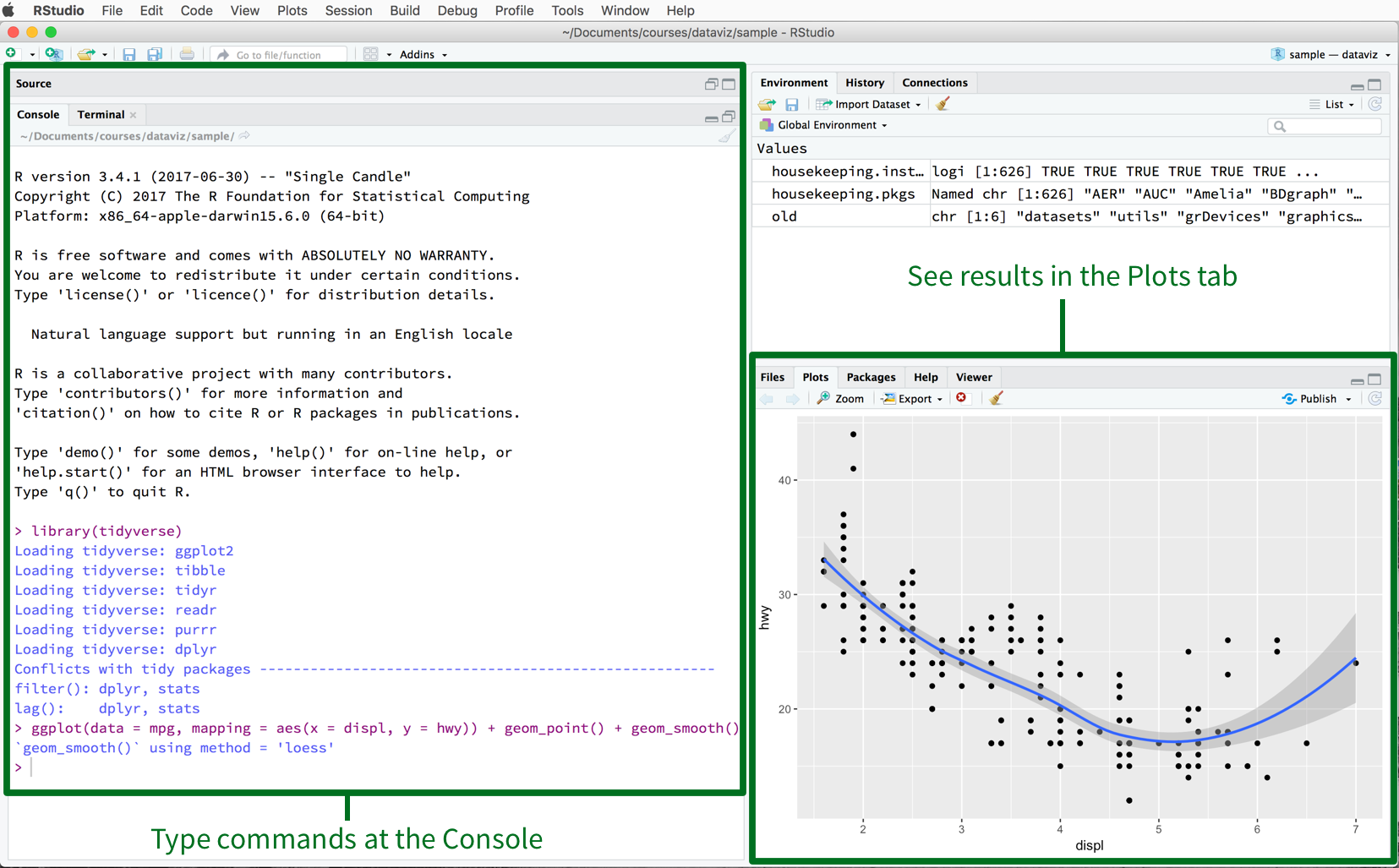
RStudio

R is an interpreter with which you interact using a text console.

You can use it in RStudio, an IDE with many features.

  • Built in console

  • Built in image viewer

  • Editor with auto-completion, syntax highlighting and all the nice things

Data types

R has five basic data types:

character

"hello"
[1] "hello"

numeric (a.k.a. real numbers, double)

0.82
[1] 0.82

integer

42L
[1] 42

complex

3.2 + 5.2i
[1] 3.2+5.2i

logical (a.k.a. booleans)

TRUE # Same as T
[1] TRUE
F # Same as FALSE
[1] FALSE

Names

In R, everything can be given a name.

x  
# this is a valid name
descriptive_name   
# descriptive names are preferable
# - note the underscore separating the words
# - spaces are not allowed
also.valid  
# This is also a valid name, using an older and maybe
# confusing naming scheme. If you come from Java/C++/Python/Javascript....
# the . in the middle of the name is *not* the member access operator

These names (and others) are not allowed.

FALSE, TRUE, Inf, NA, NaN, NULL, for, if, else, break, function

Some names are best avoided, because they are library functions that you would overwrite.

mean, range

Binding things to names

Using the “arrow” syntax you can assign names to things.

x <- 5  # The `arrow` is the assignment operator
some_string <- "Hello I am a sequence of characters"

Later, you can retrieve the values by referencing the name.

x
[1] 5
some_string
[1] "Hello I am a sequence of characters"

Using R as a calculator

Arithmetic

# addition, subtraction, multiplication, division
  +         -            *               /

# quotient, remainder
  %/%       %%

# power
  ^

Comparisons

<  >   <=  >=  ==  !=

Logical

# NOT   
  !
# short-circuited AND    short-circuited OR   <- for control flow
  &&                     ||
# AND                    OR                   <- for logical operations
  &                      |

Boolean values and comparisons

# Boolean and
TRUE & FALSE
[1] FALSE
# Boolean or
TRUE | FALSE
[1] TRUE
# Negation
!TRUE
[1] FALSE
5 == 3
[1] FALSE
5 != 3
[1] TRUE
5 > 3
[1] TRUE
5 <= 3
[1] FALSE
!(5 < 3) & (TRUE & (2*2 == 4))
[1] TRUE

Using R as a calculator

What does the following comparison return (sqrt gives the square root)?

sqrt(2)^2 == 2

\[ (\sqrt{2})^2 = 2 \]

[1] FALSE

numeric data is insidious;
comparisons should be handled with care.

sqrt(2)^2 - 2
[1] 4.440892e-16
dplyr::near(sqrt(2)^2, 2)
[1] TRUE

Missing values

The NA keyword represents a missing value.

NA > 3
[1] NA
NA + 10
[1] NA
NA == NA
[1] NA

Missing values

To check if a value is NA you use the is.na function.

a <- NA
is.na(a)
[1] TRUE
b <- "this variable has a value"
is.na(b)
[1] FALSE

Other special values

What is the result of this operation?

0 / 0
[1] NaN

The NaN value (Not a Number): the result cannot be represented by a computer.

What about this operation?

sqrt(-1)
[1] NaN

We get NaN even if this would be the definition of the complex number i.

If you want the complex number, then you should declare it explicitly.

sqrt( as.complex(-1) )
[1] 0+1i

NA vs NaN

Beware: in R the values NA and NaN refer to distinct concepts.

This is in contrast with Python, where NaN is often used also to indicate missing values.

In particular, and confusingly

is.na(NaN)
[1] TRUE

but

is.nan(NA)
[1] FALSE

Other special values

What about this operation?

1 / 0
[1] Inf

The Inf value is used to represent infinity, and propagates in calculations.

Inf + 10
[1] Inf
min(Inf, 10)
[1] 10
Inf - Inf
[1] NaN

Vectors

Atomic vectors are homogeneous indexed collections of values of the same basic data type.

vec_numbers <- vector("numeric", 4)
vec_numbers
[1] 0 0 0 0
vec_letters <- vector("character", 6)
vec_letters
[1] "" "" "" "" "" ""

You can also define sequence of numbers

1:10
 [1]  1  2  3  4  5  6  7  8  9 10

Vectors

You can ask for the type of a vector using typeof.

typeof(vec_numbers)
[1] "double"
typeof(vec_letters)
[1] "character"
typeof(1:10)
[1] "integer"

Vectors

You can ask for the length of a vector using length.

length(vec_numbers)
[1] 4
length(vec_letters)
[1] 6
length(1:10)
[1] 10

What about scalars?

What does this return?

typeof(3)
[1] "double"

What about this?

length(3)
[1] 1

There are no scalar values, but vectors of length 1!

Vectors

The c function combines its arguments.

c(1, 5, 3, 6, 3)
[1] 1 5 3 6 3

What does this code do?

nums_a <- c(1,3,5,7)
nums_b <- c(2,4,6,8)
c(nums_a, nums_b)
[1] 1 3 5 7 2 4 6 8

Using c multiple times does not nest vectors

Vectors

What about this code?

c(1, "hello", 0.45)
[1] "1"     "hello" "0.45" 
typeof(c(1, "hello", 0.45))
[1] "character"

This is called implicit coercion.

It converts all the elements to the type that can represent all of them.

Coercion

42L + 3.3
[1] 45.3
3 + "I'm a stringy string"
Error in 3 + "I'm a stringy string": non-numeric argument to binary operator
"ahahaha" & T
Error in "ahahaha" & T: operations are possible only for numeric, logical or complex types

Recycling

Recycling

What do you think will happen with this code?

c(1, 2, 3) + 1
[1] 2 3 4

R coerces the length of vectors, if needed.

Remember that 1 is a vector of length one.

By coercion, in the operation above, it is replaced with c(1, 1, 1) by recycling its value.

So what about this?

c(1, 2, 3) + c(1, 3)
[1] 2 5 4

Operations on logical vectors

There are distinct operators for element-wise operators on logical vectors:

c(T, T, F) & c(T, F, T)
[1]  TRUE FALSE FALSE

which is different from

# c(T, T, F) && c(T, F, T)

If you want to check if all the values are true in a vector, you can use the function all:

all(c(T, T, T))
[1] TRUE

or the function any to check if at least one value is true

any(c(F, T, F))
[1] TRUE

Operations on logical vectors

How can you check if all the values are FALSE?

To check if all the values are false, you can negate the vector

lgls <- c(F, F, F)
all(!lgls)
[1] TRUE

Naming vectors

Elements of vectors can be named, which will be useful for indexing into the vector.

named_vec <- c(
  Alice         = "swimming",
  Bob           = "playing piano",
  Christine     = "cooking",
  Daniel        = "singing",
  "Most people" = "eating"
)

Notice that you need to enclose a name in quotes only if it contains spaces.

Subsetting vectors

You can index into vectors using integer indexes.

Beware: indexing starts from 1!

myvec <- c("these", "are", "some", "values")
myvec[3]
[1] "some"

So what about this?

myvec[0]
character(0)

And this?

myvec[5]
[1] NA

Subsetting vectors

Subsetting vectors

myvec <- c("these", "are", "some", "values")

myvec[c(1,2,4)]
[1] "these"  "are"    "values"

What does the code below give?

myvec[c(4,1)]
[1] "values" "these"

And the following?

myvec[c(1,1,3,3,1)]
[1] "these" "these" "some"  "some"  "these"

Subsetting vectors

myvec <- c("these", "are", "some", "values")

What about

myvec[-2]
[1] "these"  "some"   "values"

Negative indices remove values from a vector!

You can of course use vectors of negative indexes

myvec[c(-1, -2)]
[1] "some"   "values"

Subsetting vectors

myvec <- 1:10

You can use boolean vectors to retain only the entries corresponding to TRUE.

myvec[myvec %% 2 == 0]
[1]  2  4  6  8 10

Subsetting and naming

Is the following naming valid?

logical_naming <- c(
  T = "a value",
  F = "another value",
  T = "a third value?"
)
logical_naming[T]
               T                F                T 
       "a value"  "another value" "a third value?"

It’s valid naming, but not useful for subsetting.

Subsetting and naming

Is the following naming valid?

logical_naming <- c(
  1 = "a value",
  2 = "another value",
  5 = "a third value?"
)

This is not valid, since it makes subsetting ambiguous.

Heterogeneous collections

A list allows to store elements of different type in the same collection, without coercion.

my_list <- list(
  3.14, "c", 3L, TRUE
)
typeof(my_list[1])
[1] "list"

What??? The type should be a double.

If you want to get atomic values, you have to index [[ to index.

typeof(my_list[[1]])
[1] "double"
typeof(my_list[[2]])
[1] "character"

Named, nested lists

my_named_list <- list(
  pi = 3.14,
  name = "Listy List",
  geo = list(
    city = "Bozen",
    country = "Italy"
  )
)

To access, either use a chain of [[

my_named_list[["geo"]][["city"]]
[1] "Bozen"

or use the $ operator

my_named_list$geo$city
[1] "Bozen"

Looking at the structure of nested lists

With the str function you can look at the structure of nested lists.

str(my_named_list)
List of 3
 $ pi  : num 3.14
 $ name: chr "Listy List"
 $ geo :List of 2
  ..$ city   : chr "Bozen"
  ..$ country: chr "Italy"

Going to higher dimensions: matrix

R support matrices out of the box. The following matrix

\[ \left[ \begin{matrix} 1 & 3 \\ 2 & 4 \end{matrix} \right] \]

can be specified as follows.

matrix(c(1,2,3,4), nrow=2, ncol=2)
     [,1] [,2]
[1,]    1    3
[2,]    2    4

Transposing and concatenating

Consider the following two matrices.

a <- matrix(c(1,2,3,4), nrow=2, ncol=2)
b <- matrix(c(11,12,13,14), nrow=2, ncol=2)

Transpose

t(a)
     [,1] [,2]
[1,]    1    2
[2,]    3    4

Concatenate

cbind(a, b)
     [,1] [,2] [,3] [,4]
[1,]    1    3   11   13
[2,]    2    4   12   14
rbind(a, b)
     [,1] [,2]
[1,]    1    3
[2,]    2    4
[3,]   11   13
[4,]   12   14

Indexing matrices

m <- matrix(c(1,2,3,4,5,6), nrow=2, ncol=3)
m
     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

Getting a single element

m[1,3]
[1] 5

Getting a row

m[1,]
[1] 1 3 5

Getting a column

m[,2]
[1] 3 4

What if you ask for out of bounds indices?

Linear algebra operations on matrices

Element-wise multiplication

a * b
     [,1] [,2]
[1,]   11   39
[2,]   24   56

Matrix multiplication

a %*% b
     [,1] [,2]
[1,]   47   55
[2,]   70   82

Inverse

solve(a)
     [,1] [,2]
[1,]   -2  1.5
[2,]    1 -0.5
a %*% solve(a)
     [,1] [,2]
[1,]    1    0
[2,]    0    1

The call to solve(a) is equivalent to

\[ A X = I \]

Control flow

Control flow: if

if (condition) {
  # Do something if condition holds
} else if (second condition) {
  # Otherwise, do something else if the second condition holds
} else {
  # If non of the previous holds, do this
}

For example, do different things depending on the type of a vector

my_vec <- c(1.0, 3.14, 5.42)

if (is.numeric(my_vec)) {
  mean(my_vec)
} else {
  # Signal an error and stop execution
  stop("We are expecting a numeric vector!")
}
[1] 3.186667

Control flow: for loops

for (iteration specification) {
  # Do something for each iteration
}

We will use the following data as examples.

loop_data <- list(
  a = rnorm(10),
  b = runif(10),
  c = rexp(10),
  d = rcauchy(10)
)
str(loop_data)
List of 4
 $ a: num [1:10] -1.207 0.277 1.084 -2.346 0.429 ...
 $ b: num [1:10] 0.317 0.303 0.159 0.04 0.219 ...
 $ c: num [1:10] 0.877 0.0146 1.8351 0.5193 1.9963 ...
 $ d: num [1:10] -159.354 -1.608 21.193 0.963 -0.907 ...

Control flow: for loops

We want to compute the mean of each of a, b, c and d in loop_data.

A straighforward approach would be

data_means <- list(
  a = mean(loop_data$a),
  b = mean(loop_data$b),
  c = mean(loop_data$c),
  d = mean(loop_data$d)
)
str(data_means)
List of 4
 $ a: num -0.383
 $ b: num 0.417
 $ c: num 0.855
 $ d: num -20.9

What are the issues with this approach?

  • Much repetition
  • We must modify the code if we ever extend the list.

Control flow: for loops

We can do better with a for loop

data_means <- list()
for (i in 1:length(loop_data)) {
  data_means <- c(
    data_means,
    mean(loop_data[[i]])
  )
}

str(data_means)
List of 4
 $ : num -0.383
 $ : num 0.417
 $ : num 0.855
 $ : num -20.9

Did we lose something?

Control flow: for loops

data_means <- list()
for (name in names(loop_data)) {
  data_means[name] = mean(loop_data[[name]])
}

str(data_means)
List of 4
 $ a: num -0.383
 $ b: num 0.417
 $ c: num 0.855
 $ d: num -20.9

Functions

Functions

Whenever you find yourself copy-pasting the code, create a function instead!

  1. The name of the function serves to describe its purpose.

  2. Maintenance is easier: you only need to update code in one place.

  3. You don’t make silly copy-paste errors.

Functions: anatomy

Function call

fn_name(<value1>,
        argument2 = <value2>)

Function definition

my_func <- function(arg1, arg2, named_arg3 = 42) {
  # Do things with arguments
  # The last statement is the return value
  # you can also use the explicit `return(value)` to do early returns
}

Functions: an example

Consider the following data

my_list <- list(
  a = rnorm(5),
  b = rcauchy(5),
  c = runif(5),
  d = rexp(5)
)
str(my_list)
List of 4
 $ a: num [1:5] 0.00986 0.67827 1.02956 -1.72953 -2.20435
 $ b: num [1:5] -1.319 1.453 -37.231 0.164 -4.862
 $ c: num [1:5] 0.1215 0.8928 0.0146 0.7831 0.09
 $ d: num [1:5] 0.0384 1.2302 2.2003 0.9757 0.337

we want to rescale all the values so that they lie in the range 0 to 1.

Functions: an example

Let’s first see how to do it on my_list$a:

maxval <- max(my_list$a)
minval <- min(my_list$a)

(my_list$a - minval) / (maxval - minval)
[1] 0.6846843 0.8913725 1.0000000 0.1468252 0.0000000

Functions: an example

Now, instead of copying and pasting the code for all the entries in my_list,

we define a function rescale01

rescale01 <- function(values) {
  maxval <- max(values)
  minval <- min(values)
  
  (values - minval) / (maxval - minval)
}

and then we can invoke it, maybe in a loop.

output <- list()
for (nm in names(my_list)) {
  output[[nm]] <- rescale01(my_list[[nm]])
}
str(output)
List of 4
 $ a: num [1:5] 0.685 0.891 1 0.147 0
 $ b: num [1:5] 0.928 1 0 0.967 0.837
 $ c: num [1:5] 0.1217 1 0 0.8751 0.0858
 $ d: num [1:5] 0 0.551 1 0.434 0.138

Functions: variable number of arguments

You can write functions that accept a variable number of arguments using the ... syntax:

with_varargs <- function(...) {
  # The following line stores the additional arguments in a list,
  # for convenient access. Additional arguments can even be named
  args <- list(...)

  return(str(args))
}
with_varargs(
  "hello",     # This is a positional argument
  b = 42,      # This is an additional argument that will go in the args list
  a = "world"  # And additional arguments can also be named
)
List of 3
 $  : chr "hello"
 $ b: num 42
 $ a: chr "world"

Libraries

Libraries

  • Functions are the basic unit of code reuse,

  • Libraries (also called packages) group together functions with related functionality.

  • https://cran.r-project.org.

Installing libraries

Just use the command

renv::install("name_of_the_library")

The tidyverse

R packages for data science

The tidyverse is an opinionated collection of R packages designed for data science.

All packages share an underlying

  • design philosophy,
  • grammar, and
  • data structures.

Install the complete tidyverse with:

renv::install("tidyverse")

Using libraries

Prepend the package name.

readr::read_csv("file.csv")

Bring all the package’s functions into scope.

library(readr)
read_csv("file.csv")

Using libraries

The second option is more convenient.

However, some names may mask the names already in scope.

library(dplyr)
Attaching package: ‘dplyr’

The following objects are masked 
from ‘package:stats’:

    filter, lag

The following objects are masked
from ‘package:base’:

    intersect, setdiff, setequal, union

In this case the shadowed names are still accessible using their fully qualified name.

stats::filter
base::intersect

Renv

Helping with reproducibility

Scenario

Imagine the following situation.

  • You install some libraries.

  • You develop a program using those libraries.

  • You send the program to someone else.

  • The program breaks in mysterious and subtle ways.

Scenario 2

Imagine the following situation.

  • You install some libraries.

  • You develop a program using those libraries.

  • You start a new project, for which you need an updated version of the libraries.

  • After a while, you go back to your first project, and it’s broken in mysterious and sublte ways!

Problems

  • Libraries change the way they work from one version to the other.
  • To get consistent results:
    • be explicit about their versions;
    • isolate projects.
  • install.packages by itself is not enough:
    • always installs the latest version;
    • installed packages are shared between all projects.

Renv to the rescue!

  • renv (for Reproducible environments) is a system to manage dependencies in a saner way.

  • It allows you to install your dependencies inside your working directory.

  • Your project now contains:
    • your code,
    • all your dependencies.

  • You can share this bundle with others and they will be able to build an exact copy of your environment.

  • All your projects can depend on different versions of the same libraries.

Using renv

Install (just once).

install.packages("renv")

Initialize.

renv::init()

Install your dependencies.

renv::install("tidyverse")

Snapshot.

renv::snapshot()

Restore missing libraries.

renv::restore()

This is run automatically when you open a renv-managed project.

The Tidyverse libraries

The Tidyverse

The tidyverse is an opinionated collection of R packages designed for data science. All packages share an underlying design philosophy, grammar, and data structures.

These packages can be installed simply by using

renv::install("tidyverse")

And then used with

library(tidyverse)

The main library we will deal with.

Declarative graphics with a well-defined grammar.

The main reason we use R rather than python.

The tabular data representation we will mostly use.

A modern iteration on the data frame concept.

Data manipulation library.

Covers most of our preprocessing needs.

Reads a variety of file formats in a convenient way.

Handles corner cases and encodings for you.

Data Visualization and Exploration - Introduction to R - ozan-k.com