Corsi di Laurea in Ingegneria Aerospaziale, Chimica, Elettrica,
dei Materiali, Meccanica e Nucleare
Corso di Fondamenti di Informatica - A.A. 1999/2000
Elenco degli esercizi per lo svolgimento dei progetti

Estratti da D. Calvanese, P. Liberatore, F. Massacci, R. Rosati.
Complementi ed esercizi di programmazione in PASCAL.
Esculapio Progetto Leonardo, seconda edizione, 1999

Esercizi sulle matrici

Esercizio 4.1   Scrivere una procedura di scrittura di matrice su file.$\Box$

Esercizio 4.2   La funzione che determina se una matrice è un quadrato magico non è ottimizzata, dal momento che vengono eseguite tutte le somme delle righe, delle colonne e delle diagonali anche se per esempio la somma delle prime due righe è differente. L'efficienza del programma può venire migliorata in due modi:

1.

Alla fine del ciclo sulle righe, se mag=FALSE allora non si esegue tutto il resto. Lo stesso alla fine del ciclo sulle colonne e della verifica della diagonale principale.

2.

All'interno di ogni ciclo, si può uscire appena mag=FALSE. Questo può venire realizzato sostituendo le istruzioni for con istruzioni while, come già visto in precedenza.

Implementare le due ottimizzazioni della funzione che determina se una matrice è un quadrato magico.$\Box$

Esercizio 4.3   Scrivere una funzione che calcoli la somma di tutti gli elementi di una matrice a valori interi.$\Box$

Esercizio 4.4   Scrivere una funzione che determini quale è la riga di una matrice la cui somma degli elementi è massima.$\Box$

Esercizio 4.5   Scrivere una funzione che determini se due matrici sono uguali.$\Box$

Esercizio 4.6   Scrivere una funzione che determini se una matrice coincide con un'altra ruotata di $90^\circ$.$\Box$

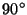
Esercizio 4.7   La funzione di verifica degli elementi nulli su una riga data nella sezione precedente è corretta, ma non ottimizzata. Infatti, se si trova un elemento non nullo non è necessario continuare la scansione. Fornire una versione ottimizzata di tale procedura.$\Box$

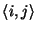
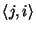
Esercizio 4.8   Una matrice quadrata si dice simmetrica se per ogni coppia di indici i e j l'elemento $\langle i,j\rangle$ è uguale all'elemento $\langle j,i\rangle$. Scrivere una funzione che verifichi se una matrice quadrata è simmetrica.$\Box$

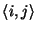
Esercizio 4.9   Una matrice quadrata si dice triangolare superiore se tutti gli elementi $\langle i,j\rangle$ con i minore di j (cioè che stanno ``sotto'' alla diagonale principale) hanno valore nullo. Scrivere una funzione che verifichi se una matrice quadrata è triangolare superiore.$\Box$

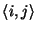
Esercizio 4.10   Una matrice quadrata si dice triangolare inferiore se tutti gli elementi $\langle i,j\rangle$ con i maggiore di j (cioè che stanno ``sopra'' alla diagonale principale) hanno valore nullo. Scrivere una funzione che verifichi se una matrice quadrata è triangolare inferiore.$\Box$

Esercizio 4.11   Scrivere una funzione che restituisca il vettore delle somme delle righe di una matrice, cioè un vettore che per ogni riga della matrice ha un elemento il cui valore è pari alla somma degli elementi della riga.$\Box$

Esercizio 4.12   Scrivere una procedura che restituisca il vettore delle somme delle colonne di una matrice.$\Box$

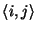
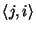
Esercizio 4.13   La trasposta di una matrice N x M è una matrice M x N tale che per ogni coppia di indici i e j il valore dell'elemento $\langle i,j\rangle$ della trasposta è pari al valore dell'elemento $\langle j,i\rangle$ della matrice. Scrivere una procedura che restituisca la trasposta di una matrice.$\Box$

Esercizi sulle liste

Esercizio 5.1   Si forniscano due implementazione della procedura CancellaElementoLista utilizzando la tecnica del record generatore, e rispettivamente 1 puntatore e 2 puntatori per la scansione della lista in ingresso.$\Box$

Esercizio 5.2   Si implementi una procedura ConcatenaListe, che prenda in ingresso due liste e restituisca la lista ottenuta per concatenazione delle due liste.

1.

Si implementi ConcatenaListe con condivisione di memoria ed in modo distruttivo sulla prima lista utilizzando l'intestazione

procedure ConcatenaListe (var lis1: TipoLista;
                          lis2: TipoLista);

``Con condivisione di memoria ed in modo distruttivo sulla prima lista'' significa che lis2 va attaccata in coda a lis1.

2.

Si implementi ConcatenaListe con condivisione di memoria (rispetto alla seconda lista) ed in modo non distruttivo utilizzando l'intestazione

procedure ConcatenaListe (lis1, lis2: TipoLista;
                          var lis3: TipoLista);

``Con condivisione di memoria (rispetto alla seconda lista) ed in modo non distruttivo'' significa che lis1 va prima copiata in lis3 e poi lis2 va attaccata in coda a lis3.

3.

Si implementi ConcatenaListe senza condivisione di memoria ed in modo non distruttivo utilizzando l'intestazione

procedure ConcatenaListe (lis1, lis2: TipoLista;
                          var lis3: TipoLista);

``Senza condivisione di memoria ed in modo non distruttivo'' significa che che lis1 va prima copiata in lis3 e poi una copia di lis2 va attaccata in coda a lis3.

Per ognuno dei casi si fornisca un'implementazione iterativa, una ricorsiva ed una utilizzando le procedure e funzioni (anche non primitive) già sviluppate.$\Box$

Esercizio 5.3   Si implementi una funzione EsisteInListaOrdinata, che prenda in ingresso una lista con gli elementi in ordine crescente ed un elemento e restituisca TRUE se l'lemento compare nella lista e FALSE altrimenti. Rispetto alla funzione EsisteInLista si sfrutti il fatto che la lista è ordinata per interrompere la scansione della lista quando si arriva ad un elemento maggiore di quello da cercare. In questo caso l'elemento non può sicuramente comparire nel resto della lista.$\Box$

Esercizio 5.4   Si implementi una procedura CancellaElementoListaOrdinata, che prenda in ingresso una lista con gli elementi in ordine crescente ed un elemento e restituisca la lista modificata avendo cancellato la prima occorrenza dell'elemento. Si sfrutti anche in questo caso il fatto che la lista è ordinata.$\Box$

Esercizio 5.5   Si implementino procedure o funzioni PASCAL che realizzano le seguenti funzionalità su liste rappresentate tramite record e puntatori. Si utilizzi per ogni procedura o funzione una intestazione opportuna e si forniscano diverse implementazioni (iterative, ricorsive ed utilizzando le funzioni elementari e/o non elementari) adottando le tecniche di programmazione mostrate nel presente capitolo:

1.

somma e/o media degli elementi di una lista di interi;

2.

conteggio del numero di volte che un dato elemento compare in una lista;

3.

lunghezza della massima sequenza di elementi uguali ad un dato elemento;

4.

lunghezza della massima sequenza di elementi consecutivi uguali;

5.

inserimento di un elemento dopo un elemento dato;

6.

cancellazione di tutti gli elementi pari da una lista di interi;

7.

cancellazione dell'ultimo elemento di una lista;

8.

cancellazione dell'ultima occorrenza di un dato elemento da una lista;

9.

cancellazione di tutti gli elementi di ordine pari da una lista (cioè del secondo, del quarto, etc.);

10.

cancellazione di tutti gli elementi di ordine dispari da una lista (cioè del primo, del terzo, etc.);

11.

cancellazione di tutte le occorrenze successive alla prima di un dato elemento;

12.

cancellazione di tutte le occorrenze successive alla prima di tutti gli elementi;

13.

creazione di una lista che contenga gli stessi elementi di una lista passata come parametro, ma in ordine inverso;

14.

[Difficile] inversione di una lista, realizzata attraverso l'inversione dei puntatori senza allocare o deallocare nuovi record.

$\Box$

Esercizio 5.6   Una lista si dice prefisso di una lista se coincide con la parte iniziale di (ma può eventualmente contenere altri elementi che seguono questa parte iniziale). Una lista si dice postfisso di una lista se coincide con la parte finale di (ma può eventualmente contenere altri elementi che precedono questa parte finale). Una lista si dice sottolista di una lista se coincide con una parte di (ma può eventualmente contenere elementi che precedono ed altri che seguono questa parte). Si forniscano diverse implementazioni in PASCAL (iterative, ricorsive ed utilizzando le funzioni elementari e/o non elementari) delle seguenti procedure e/o funzioni:

1.

funzione che verifica se una lista è prefisso di un'altra lista;

2.

funzione che verifica se una lista è posfisso di un'altra lista;

3.

funzione che verifica se una lista è sottolista di un'altra lista.

4.

procedura che cancella da una lista un prefisso di una data lunghezza;

5.

procedura che cancella da una lista un postfisso di una data lunghezza;

6.

procedura che in una lista cancella da una data posizione in poi una sottolista di una data lunghezza;

7.

procedura che in una lista cancella da un dato elemento in poi una sottolista di una data lunghezza;

8.

procedura che sostituisce in una lista un prefisso di lunghezza pari alla lunghezza di una lista con ;

9.

procedura che sostituisce in una lista un postfisso di lunghezza pari alla lunghezza di una lista con ;

10.

[Difficile] procedura che sostituisce in una lista un prefisso di una data lunghezza con una lista ;

11.

[Difficile] procedura che sostituisce in una lista un postfisso di una data lunghezza con una lista ;

12.

[Difficile] procedura che sostituisce in una lista una sottolista di con una lista .

$\Box$

Esercizio 5.7   Si forniscano diverse implementazioni in PASCAL (iterative, ricorsive ed utilizzando le funzioni elementari e/o non elementari) di procedure che effettuano l'ordinamento di una lista. Si utilizzino gli algoritmi di ordinamento su vettori presentati nel capitolo 9 Si forniscano:

1.

[Difficile] implementazioni che effettuano scambi tra i campi info dei record contenenti gli elementi della lista, senza modificare i puntatori della lista;

2.

[Molto difficile] implementazioni che effettuano scambi tra i puntatori dei record contenenti gli elementi della lista, senza modificare i campi info della lista;

$\Box$

Varianti di esercizi di esame sulle matrici

Sezione 10.1

Esercizio 10.1   Modificare la procedura richiesta al punto (2) in modo tale che restituisca il valore vero se in T esistono k posti liberi, non necessariamente adiacenti, su una riga con costo unitario $\leq q$.$\Box$

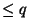
Esercizio 10.2   Modificare la procedura richiesta al punto (2) in modo tale che restituisca il valore vero se in T esistono k posti liberi, non necessariamente adiacenti e non necessariamente sulla stessa riga, con costo unitario $\leq q$.$\Box$

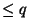
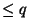
Esercizio 10.3   Modificare la procedura richiesta al punto (2) in modo tale che restituisca il valore vero se in T esistono k posti liberi adiacenti con costo unitario $\leq q$, dove per adiacenti si intendono, oltre a due posti successivi sulla stessa riga, anche l'ultimo posto (colonna m) di una riga ed il primo posto (colonna 1) della riga successiva.$\Box$

Sezione 10.2

Esercizio 10.4   Modificare la procedura richiesta al punto (2) in modo che stampi la lettera (o le lettere) che compare il maggior numero di volte nelle copie degli elementi di stampa a disposizione.$\Box$

Esercizio 10.5   Modificare la procedura richiesta al punto (3) in modo che funzioni anche con parole composte da un numero dispari di caratteri. Per questo tipo di parole, la stampa dell'ultimo carattere può avvenire utilizzando una qualsiasi coppia che ha come primo carattere l'ultimo carattere della parola.$\Box$

Sezione 10.4

Esercizio 10.6   Modificare la procedura proposta al punto (1) in modo tale che esca dal ciclo di scansione non appena:

a)

si è trovato un elemento dominante;

b)

non si può più trovare un elemento dominante perché si è già scandita più di metà della matrice.

$\Box$

Esercizio 10.7   Modificare la procedura proposta al punto (1) in modo tale che i due cicli for più interni vengano eseguiti solo se l'elemento corrente dei cicli più esterni (m[i,j]) è un carattere che non era già stato considerato in precedenza. Si utilizzi a tale scopo una matrice di valori booleani, per tenere traccia degli elementi già considerati.$\Box$

Varianti di esercizi di esame sulle liste

Sezione 11.1

Esercizio 11.1   Modificare la procedura sviluppata al punto (2) in modo da riutilizzare la memoria occupata dagli insiemi in ingresso per la creazione dell'insieme unione. Le liste in ingresso vanno perdute, e la memoria occupata da eventuali elementi non utilizzati deve essere di nuovo resa disponibile.$\Box$

Esercizio 11.2   Si scriva una procedura PASCAL che, ricevendo in due parametri di ingresso due insiemi rappresentati mediante liste semplici, fornisca in un parametro di uscita l'intersezione degli insiemi dati, nella stessa rappresentazione, creando una nuova lista senza modificare gli insiemi dati.$\Box$

Esercizio 11.3   Si scriva una procedura PASCAL che, ricevendo in un parametro di ingresso un insieme rappresentato tramite vettore caratteristico, fornisca in un parametro di uscita lo stesso insieme rappresentato mediante lista semplice.$\Box$

Sezione 11.4

Esercizio 11.4   Scrivere una procedura PASCAL che, ricevendo come parametri di input un numero di inventario e un numero di utente, aggiorni la lista dei prestiti dell'utente, eliminando (se esiste) il record con il numero di inventario in input nella lista dei prestiti dell'utente il cui numero è ricevuto in input dalla procedura.$\Box$

Sezione 11.5

Esercizio 11.5   Scrivere una procedura PASCAL che, ricevendo come parametro di input l'immagine in forma compatta prodotta dalla procedura richiesta al punto (2), crei una rappresentazione compatta dell'immagine ottenuta invertendo ogni riga. Ad esempio, se la riga i-esima è

         B B B B B V V V V V V G G G B B .....

la riga i-esima invertita è

         ..... B B G G G V V V V V V B B B B B

$\Box$

Sezione 11.6

Esercizio 11.6   Fornire una implementazione iterativa della procedura richiesta al punto (3).$\Box$

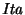
Esercizio 11.7   Modificare la procedura richiesta al punto (3) in modo tale che restituisca come parametro di uscita la lista ottenuta dalla lista di ingresso eliminando tutti i record con quantità di pioggia maggiore o uguale a .$\Box$

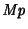
Esercizio 11.8   Modificare la procedura richiesta al punto (3), nell'ipotesi che la lista di input 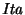non sia ordinata per quantità di pioggia decrescenti.$\Box$

Sezione 11.7

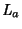
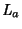
Esercizio 11.9   Si modifichi la procedura sviluppata al punto (3) in modo che, ricevendo per parametri le liste $\ensuremath{\mathit{L}}_a$ e $\ensuremath{\mathit{L}}_a$, crei la lista delle località che soddisfano entrambe le condizioni (a) e  (b) e la restituisca in un parametro di uscita. Tale lista deve essere ordinata in base alla distanza crescente dal giacimento conosciuto e ciascuna località deve occorrere una sola volta. 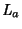La procedura deve anche stampare su standard output le località in $\ensuremath{\mathit{L}}_a$ la cui distanza dal giacimento conosciuto risulti inferiore a 100 chilometri.$\Box$

Sezione 11.8

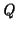
Esercizio 11.10   Si modifichi la procedura sviluppata al punto (3) in modo che effettui l'eliminazione delle rimanenze rispetto ad una soglia per tutti i generi di prodotti presenti in $\ensuremath{\mathit{L}}_a$.$\Box$

Sezione 11.9

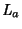
Esercizio 11.11   Estendere la funzione proposta come soluzione al punto (2) in modo che valuti correttamente un'espressione banale nella quale l'operatore `-' può comparire più volte consecutivamente.$\Box$

Esercizio 11.12   Estendere la funzione proposta come soluzione al punto (2) in modo che stampi un messaggio di errore e restituisca il valore 0 nel caso in cui la lista passata come parametro non rappresenti un'espressione banale corretta.$\Box$

Esercizio 11.13   Implementare una funzione ricorsiva che valuti un'espressione banale applicando le operazioni da destra a sinistra. Si utilizzi l'algoritmo ricorsivo fornito come soluzione errata alla funzione richiesta al punto (2).$\Box$

Esercizio 11.14   [Difficile] Scrivere una funzione ricorsiva per la valutazione di un'espressione banale come richiesto al punto (2), cioè applicando le operazioni da sinistra a destra.$\Box$

Esercizio 11.15   [Molto difficile] Scrivere una funzione (ricorsiva o iterativa) per la valutazione di un'espressione banale, tenendo conto della precedenza dell'operatore `*' sull'operatore `+'.$\Box$

Sezione 11.10

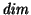
Esercizio 11.16   [Difficile] Si modifichino le procedure sviluppate ai punti (2) e (3) in modo che le righe vengano spezzate solo in prossimità degli spazi bianchi. Si ammette quindi che una riga possa contenere meno di caratteri.$\Box$

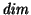
Esercizio 11.17   [Difficile] Si modifichino le procedure sviluppate ai punti (2) e (3) in modo che le righe vengano spezzate solo in prossimità degli spazi bianchi. Le righe che sono state spezzate devono essere portate tutte a lunghezza , eventualmente spaziando le parole in modo uniforme attraverso l'inserimento di spazi bianchi.$\Box$