Inductively defined domains and recursion

The elements of an inductively defined domain can be easily manipulated through recursion.

A method is said to be recursive if it contains an activation of itself (either directly, or indirectly through the activation of other methods).

Let us see some examples of mathematical functions on natural numbers that are defined inductively, exploiting the fact that these functions operate on elements of an inductively defined domain.

Example: Factorial:

fact(n) = $$\cases{ 1, & if \(n=0\) \qquad (base case)\cr n \cdot \mathit{fact}(n-1), & if \(n>0\) \qquad (recursive case)}$$

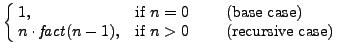
The recursive definition of a function reflects the structure of the inductive definition of the domain on which the function operates; hence we have:

• one (or more) base cases, for which the result of the function can be determined directly;
• one (or more) recursive cases, for which the computation of the result is reduced to the computation of the same function on a smaller/simpler value of the domain.

The fact that the domain on which the function operates is defined inductively guarantees us that, by repeatedly applying the recursive cases, we will reach in a finite number of steps one of the base cases.

Starting from the recursive definition of a function, we can usually provide rather easily an implementation by means of a recursive method.

Example: Implementation of the factorial by means of a recursive method:

public static long factorial(long n) {
  if (n == 0)
    return 1;
  else
    return n * factorial(n-1);
}