GCD: using the method by Euclid with rests

What happens in the previous algorithm if x is much bigger than y (or vice-versa)?

Example:

gcd(1000, 2)					gcd(1001, 500)
1000	2				1001	500
998	2				501	500
996	2				1	500
$\vdots$	$\vdots$				$\vdots$	$\vdots$
2	2				1	1

To compress this long sequence of subtractions, it is sufficient to observe that we are actually calculating the rest of the integer division.

Method by Euclid: let x = y ^. k + r (with 0 < = r < y)

gcd(x, y) = $$\cases{ y, & if $r=0$\ (i.e., $x$\ is a multiple of $y$)\cr \mathrm{gcd}(r,y), & if $r\neq 0$}$$

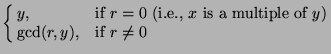
The algorithm can be implemented in Java as follows:

public static int greatestCommonDivisor(int x, int y) {
  while ((x != 0) && (y != 0)) {
    if (x > y)
      x = x % y;
    else
      y = y % x;
  }
  return (x != 0)? x : y;
}