GCD: using the method by Euclid

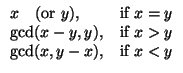
The method by Euclid allows us to reach smaller numbers faster, by exploiting the following properties:

gcd(x, y) = $$\left\{\vphantom{ \begin{array}{ll} x \quad(\mathrm{or}~y), & \... ...mbox{if } x>y\\ \mathrm{gcd}(x, y-x), & \mbox{if } x<y \end{array} }\right.$$$$\begin{array}{ll} x \quad(\mathrm{or}~y), & \mbox{if } x=y\\ ... ..., y), & \mbox{if } x>y\\ \mathrm{gcd}(x, y-x), & \mbox{if } x<y \end{array}$$

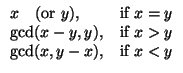
This property can be proved easily, by showing that the common divisors of x e y are also divisors of x - y (when x > y) or of y - x (when x < y).

E.g., gcd(12, 8) = gcd(12 - 8, 8) = gcd(4, 8 - 4) = 4

To obtain an algorithm, we repeatedly apply the procedure until we arrive at the situation where x = y. For example:

x	y	bigger - smaller
210	63	147
147	63	84
84	63	21
21	63	42
21	42	21
21	21	$\Longrightarrow$ gcd(21,21) = gcd(21,42) = ... = gcd(210,63)

The algorithm can be implemented in Java as follows:

public static int greatestCommonDivisor(int x, int y) {
  while (x != y) {
    if (x > y)
      x = x - y;
    else              // this means that y > x
      y = y - x;
  }
  return x;
}