The nodes are expanded according to the circled numbers. The circled (5) is the first goal node found — this is the shortest presentation that covers all the topics.

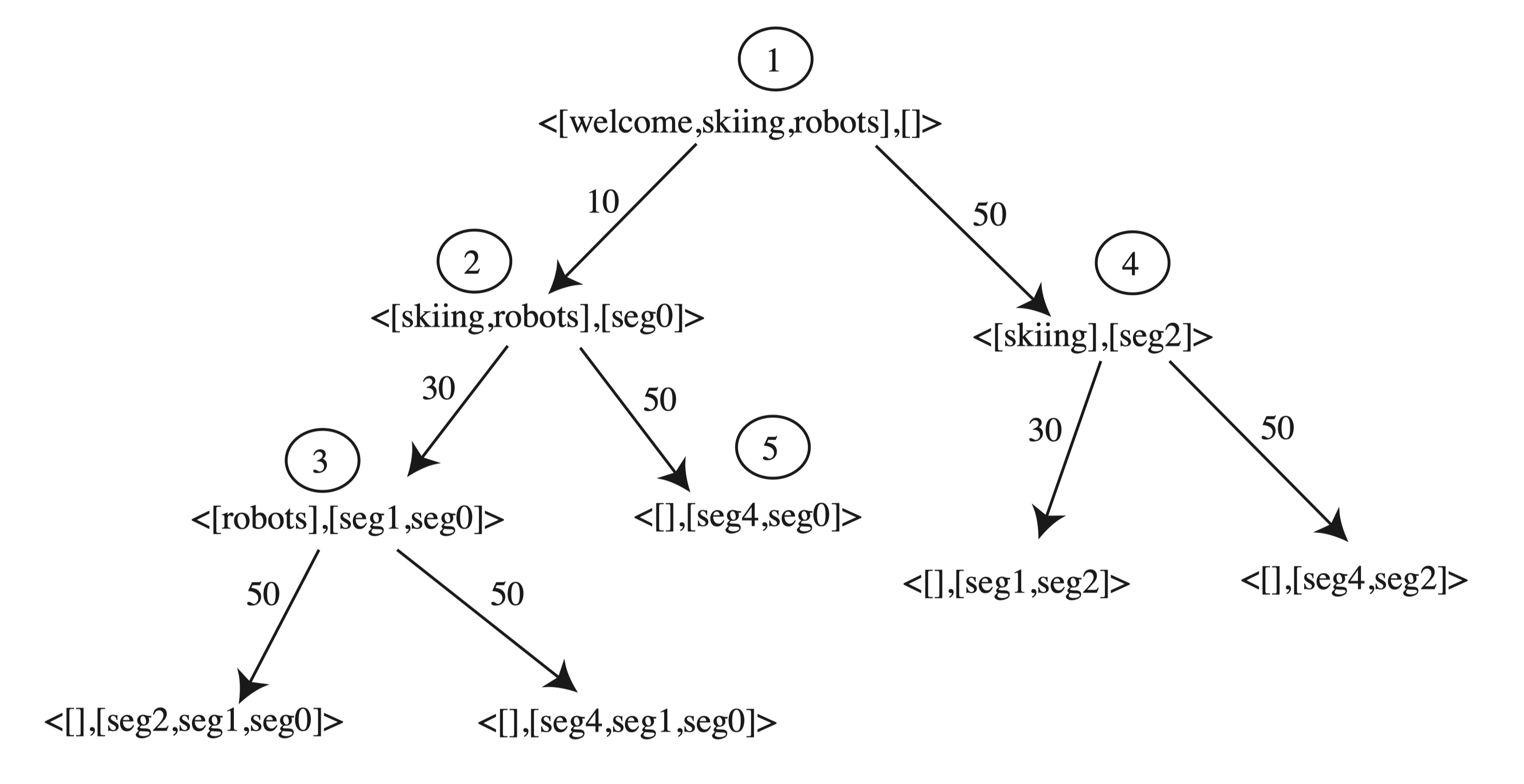
Here are two solutions:

For each topic, t, let s(t) be the length of the smallest segment that covers topic t. Let h(<TC, Segs>) = max_t∈TC s(t). That is, we find the topic t for which s(t) is maximum. Yes, it satisfies the monotone restriction as the actual distance between any two nodes is the sum of the length of the topics added between the two nodes (the only nodes that have actual distances that those where there is a path from one to the other). The difference between the h-values of the two nodes must be less than the time of the segments added to solve that goal.

For each segment let the contribution of the segment be the time of the segment divided by the number of topics the segment covers. For each topic, t, let s(t) be the smallest contribution for all of the segments that covers the topic. Let h(<TC, Segs>) = ∑_t∈TC s(t). That is, we sum s(t) for all of the topics t in TC. The intuition is that each topic t requires at least s(t) time. Note that we need to divide by the number of topics the segment covers to make sure that we do not double count the time for segments added that cover multiple topics. Yes it satisfies the monotone restriction (for similar arguments to those above).

Both of these solution require one pass through the segment database to build the s(t) function, but once this is built, the heuristic function can be computed in time proportional to the length of the To_cover list.