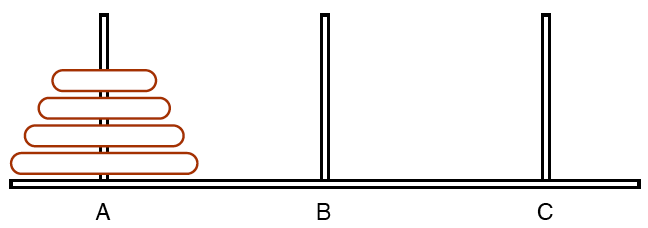
There are 3 pegs (A,B,C) and a tower of disks on the first one (A), with the smaller on the top and the bigger on the bottom. The purpose of the puzzle is to move the whole tower from the first peg (A) to the third (C), by moving only one disk every time and by observing not to put a bigger disk atop of a smaller one.

This is one of the prototypical problems that can be solved by using a recursive algorithm; however, it can be encoded as a standard search problem. In this exercise you should use a standard search problem to find the minimal sequence of disc position (states) that ends up with all the four disks on the 3rd peg (C).
Encode the problem as a standard search problem, and define an appropriate consistent heuristic to guide the search.
Encode the problem in Java and use the A* to find the solution.
In this exercise you're asked to implement and evaluate the
behaviour of an hill climbing algorithm w.r.t. the 8-queen problem.
Represent an 8-queen problem state as a list of 8 numbers, expressing
the position of a queen in the corresponding
column, counting from 1 and starting from the bottom left corner. For
example, the state in the figure below corresponds to the list [1,
6, 2, 5, 7, 4, 8, 3].

The successor function generates all the states obtained by moving one of the 8 queens along its column. The heuristic function you should use is the number of pairs of queens attacking each other. For example, the state in the figure has an heuristic value of 1.
Implement a hill climbing search using the algorithm described
during the lecture. Choose the starting node randomly in the state
space, using an uniform distribution.
Use the same algorithm to implement a Random-Restart hill climbing
search. Use a maximum of 7 restarts per instance, choosing the random
starting nodes with an uniform distribution on the state space.