6.1.4 Expected Values
You can use the probabilities to give the expected value of any numerical random variable (i.e., one whose domain is a subset of the reals). A variable's expected value is the variable's weighted average value, where its value in each possible world is weighted by the measure of the possible world.
Suppose V is a random variable whose domain is numerical, and ω is a possible
world. Define V(ω) to be the value v in the domain
of V such that ω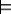 
V=v. That is, we are treating a
random variable as a function on worlds.
The expected value of numerical variable V, written E(V), is
E(V) = ∑ω∈ΩV(ω)×µ(ω)
when finitely many worlds exist. When infinitely many worlds exist, we must integrate.
E(number_of_broken_switches)
would give the expected number of broken switches. If the world acted according to the probability model, this would give the long-run average number of broken switches.
In a manner analogous to the semantic definition of conditional probability, the conditional expected value of variable X conditioned on evidence e, written E(V|e), is
E(V|e) = ∑ω∈ΩV(ω)×µe(ω).
Thus,
E(V|e) = (1)/(P(e))∑ω = ∑ω∈ΩV(ω)×P(ω|e ).
E(number_of_broken_switches|¬lit(l1)).
This is obtained by averaging the number of broken switches over all of the worlds in which light l1 is not lit.
