5.2.2 Proofs
So far, we have specified what an answer is, but
not how it can be computed. The definition of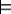 
specifies
what propositions should be logical consequences of a knowledge base but not how to compute
them. The problem of deduction is
to determine if some proposition is a logical consequence of a
knowledge base. Deduction is a specific form of inference.
A proof is a mechanically derivable demonstration that a proposition logically follows from a knowledge base. A theorem is a provable proposition. A proof procedure is a - possibly non-deterministic - algorithm for deriving consequences of a knowledge base. See the box for a description of non-deterministic choice.
Given a proof procedure, KB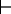 
g means g can be
proved or derived
from knowledge base
KB.
A proof procedure's quality can be judged by whether it computes what it is meant to compute.
A proof procedure is sound with respect
to a semantics if everything that can be derived from a knowledge base
is a logical consequence of the knowledge base. That is, if
KB 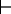g, then KB 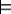g.
A proof procedure is complete with
respect to a semantics if there is a proof of each logical consequence
of the knowledge base. That is, if KB 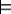g, then KB 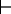g.
We present two ways to construct proofs for propositional definite clauses: a bottom-up procedure and a top-down procedure.
